Suppose an alternating series with terms that are nonincreasing in magnitude, converges to S and the sum
Question:
Suppose an alternating series 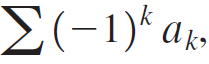 with terms that are nonincreasing in magnitude, converges to S and the sum of the first n terms of the series is Sn. Suppose also that the difference between the magnitudes of consecutive terms decreases with k. It can be shown that for n ≥ 1,
with terms that are nonincreasing in magnitude, converges to S and the sum of the first n terms of the series is Sn. Suppose also that the difference between the magnitudes of consecutive terms decreases with k. It can be shown that for n ≥ 1,
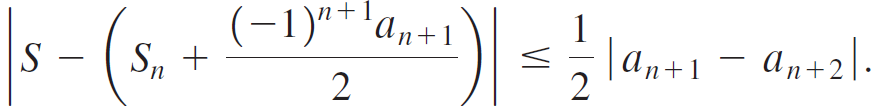
a. Interpret this inequality and explain why it is a better approximation to S than Sn.
b. For the following series, determine how many terms of the series are needed to approximate its exact value with an error less than 10-6 using both Sn and the method explained in part (a).
(i)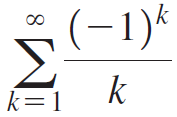
(ii)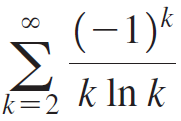
(iii) 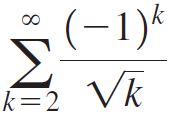
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Calculus Early Transcendentals
ISBN: 978-0321947345
2nd edition
Authors: William L. Briggs, Lyle Cochran, Bernard Gillett
Question Posted:





