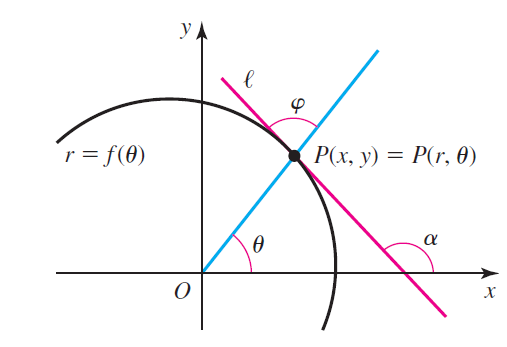
Let a polar curve be described by r = f() and let be the line tangent

Let a polar curve be described by r = f(θ) and let ℓ be the line tangent to the curve at the point P(x, y) = P(r, θ) (see figure).

a. Explain why tan α = dy/dx.

b. Explain why tan θ = y/x.

c. Let φ be the angle between ℓ and the line through O and P. Prove that tan φ = f(θ)/f'(θ).

d. Prove that the values of θ for which ℓ is parallel to the x-axis satisfy tan θ = -f(θ)/f'(θ).

e. Prove that the values of θ for which ℓ is parallel to the y-axis satisfy tan θ = f'(θ)/f(θ).

Transcribed Image Text:

УА Ф r = f(0) Р(х, у) %3D Р(r, ө) ө х