Let F = f/g be the quotient of two functions that are differentiable at x.

a. Use the definition of F' to show that

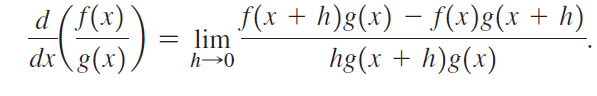
b. Now add -f(x)g(x) + f(x)g(x) (which equals 0) to the numerator in the preceding limit to obtain

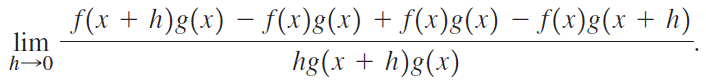
Use this limit to obtain the Quotient Rule.

c. Explain why F' = (f/g)' exists, whenever g(x) ≠ 0.

Transcribed Image Text:

d (f(x) dx\g(x) f(x + h)g(x) – f(x)g(x + h) lim hg(x + h)g(x) f(x + h)g(x) – f(x)g(x) + f(x)g(x) - f(x)g(x + h) hg(x + h)g(x) lim