Newton discovered the binomial series and then used it ingeniously to obtain many more results. Here is a case in point.

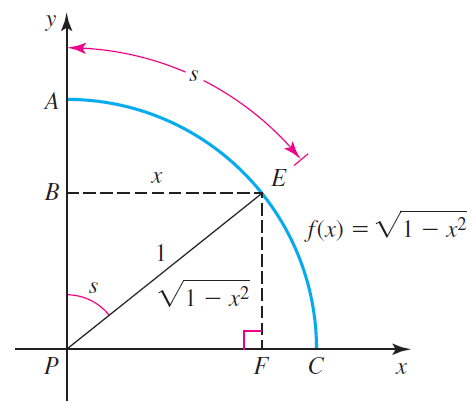
a. Referring to the figure, show that x = sin s or s = sin^-1 x.

b. The area of a circular sector of radius r subtended by an angle θ is 1/2 r² θ. Show that the area of the circular sector APE is s/2, which implies that

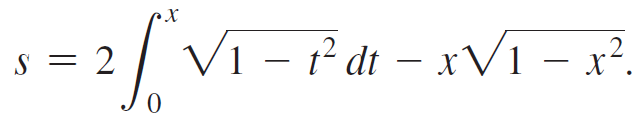
c. Use the binomial series for f(x) = √1 - x² to obtain the first few terms of the Taylor series for s = sin^-1 x.

d. Newton next inverted the series in part (c) to obtain the Taylor series for x = sin s. He did this by assuming that sin s = ∑a_ks^k and solving x = sin (sin^-1 x) for the coefficients a_k. Find the first few terms of the Taylor series for sin s using this idea (a computer algebra system might be helpful as well).

Transcribed Image Text:

x = 2/ Vi - f di – xVT – x² xV1 - x V1 – ² dt УА х B f(x) = V1 – x² V 1 x² х