Suppose f and g have Taylor series about the point a. a. If f(a) = g(a) =

Question:

Suppose f and g have Taylor series about the point a.

a. If f(a) = g(a) = 0 and g'(a) ≠ 0, evaluate |lim f(x)/g(x) |x>a by expanding f and g in their Taylor series. Show that the result is consistent with l’Hôpital’s Rule.

b. If f(a) = g(a) = f'(a) = g'(a) = 0 and g"(a) ≠ 0, evaluate 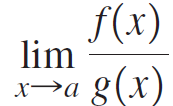f(x) lim x→a g(x) by expanding f and g in their Taylor series. Show that the result is consistent with two applications of l’Hôpital’s Rule.