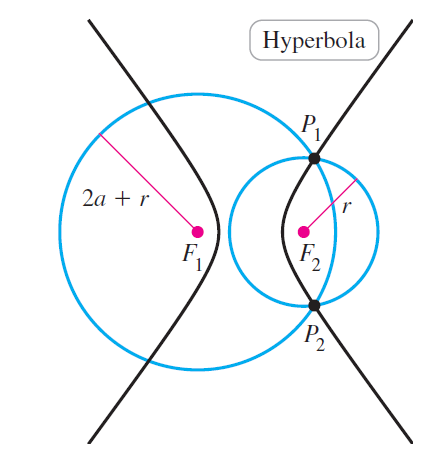
Question: Suppose two circles, whose centers are at least 2a units apart (see figure), are centered at F 1 and F 2 , respectively. The radius

Suppose two circles, whose centers are at least 2a units apart (see figure), are centered at F₁ and F₂, respectively. The radius of one circle is 2a + r and the radius of the other circle is r, where r ≥ 0. Show that as r increases, the intersection point P of the two circles describes one branch of a hyperbola with foci at F₁ and F₂.

Нуperbola 2a + r F,

perbola 2a + r F,

Step by Step Solution

★★★★★

3.26 Rating (158 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

The points on the intersection of the two circ... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Calculus Early Transcendentals Questions!

The formula used to determine the radius of the yaw mark arc is derived from a geometric relationship about two intersecting chords in a circle. In the figure, chords AB and CD intersect at point E...

Two circles of radius b intersect as shown in Figure 6 with their centers 2a apart (0 ¤ a ¤ b). Find the area of the region of their overlap. -a

Suppose a sphere of radius r is sliced by two horizontal planes h units apart (see figure). Show that the surface area of the resulting zone on the sphere is 2rh, independent of the location of the...

806 Chapter Fifteen OPTIMIZATION: LOCAL AND GLOBAL EXTREMA If f is not continuous or the region R is not closed and bounded, there is no guarantee that f achieves a global maximum or global minimum...

Convex geometry 0.1 Dehn-Sommerville relations In this section we will talk about convex polytopes. One possible denition of a convex polytope uses the notion of a half-space: A closed half-space in...

Jones & Bartlett Learning, LLC. NOT FOR RESALE OR DISTRIBUTION CHAPTER Hot Spot Analysis 10 LEARNING OBJECTIVES C A R R Provide a working definition of a \"hot spot.\" , Be able to explain different...

E-Physics Tutorial Book Note: I have attached below the lesson for the 3 activities. Thank you so much for your time and effort. Activity 1. Directions: Use the right-hand rule to determine the...

Question 2: Explain geometrically how the formula for a single A is obtained. Explain why this area depends on r and not just r. Note that this is about just a single "polar rectangle" and not the...

Fraction of hosts infected Case Study 2 Hosts, Parasites, and Time-Travel 0.8 0.6 0.4 0.2 0 Past Contemporary Future Time Figure \u00031 Horizontal axis is the time from which the parasite was taken,...

please read chapter and answer the following questions. All answers must be typed. thank you, will give thumbs up. 1. What kind of structure, controls, and culture would you be likely to find in (a)...

A student tries to solve 4x 6 -24: 4x -24 4.4 x > -6 Describe any errors. Then solve the inequality correctly.

You are the father or mother of a family of four (kids ages 13 and 15) planning a weekend camping trip. Develop a responsibility matrix for the work that needs to be done prior to starting your trip.

Here is Question 3 5 written out:Question 3 5 Charla Corporation is owned eighty percent ( 8 0 % ) by Jeanette and twenty percent ( 2 0 % ) by Victoria who are unrelated to each other. Pursuant to a...

=+How can an Internet-only company gain exposure and attract the attention

Let u = 5i - j + k, v = j - 5k, w = -15i + 3j - 3k. Which vectors, if any, are (a) Perpendicular? (b) Parallel? Give reasons for your answers.

Find the magnitude of the torque exerted by F on the bolt at P if and |F| = 30 lb . Answer in footpounds. |PQ| = 8 in.

If |v| = 2, |w| = 3, and the angle between v and w is /3, find |v - 2w|.

Consider the following two projects: Project Year 0 Year 1 Year 2 Year 3 Year 4 Cash Flow Cash Flow Cash Flow Cash Flow Cash Flow A - 100 40 50 60 N/A B -73 30 30 30 30 Discount Rate 0.1 0.1 The net...

A stock just paid a dividend of $1.03. The dividend is expected to grow at 20.05% for two years and then grow at 4.26% thereafter. The required return on the stock is 13.41%. What is the value of the...

MATH 250- Elements of Statistics Class Data, Spring 2021---CLEANED Student Data--ID# Renur Individual Foot Number Hair ID# Gender Length Height Age Armspan in Family Color Female 24.5 157.5 20 158.0...