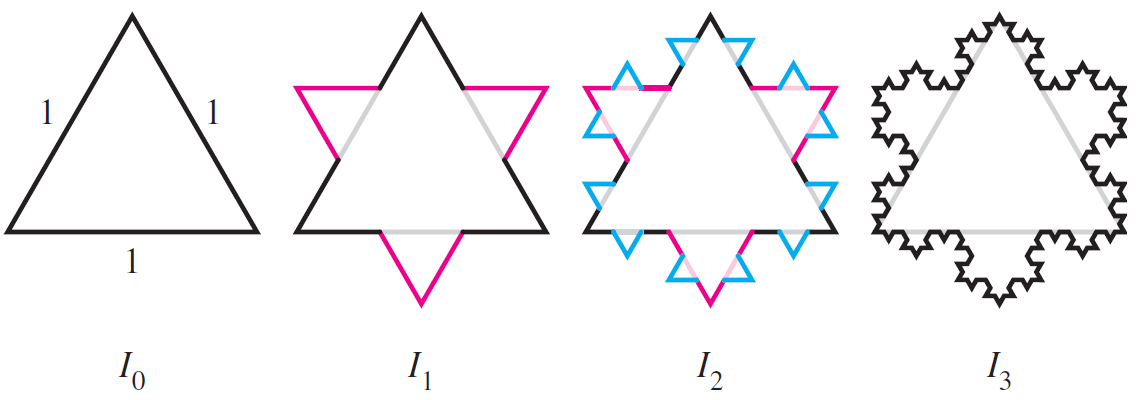
The fractal called the snowflake island (or Koch island) is constructed as follows: Let I₀ be an equilateral triangle with sides of length 1. The figure I₁ is obtained by replacing the middle third of each side of I₀ with a new outward equilateral triangle with sides of length 1/3 (see figure). The process is repeated where I_{n + 1} is obtained by replacing the middle third of each side of In with a new outward equilateral triangle with sides of length 1/3^{n + 1}. The limiting figure as n→∞ is called the snowflake island.

a. Let L_n be the perimeter of In. Show that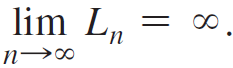

b. Let A_n be the area of I_n. Find It exists!

Transcribed Image Text:

'n, п0 lim An. 'n' п>00