The fractal called the Sierpinski triangle is the limit of a sequence of figures. Starting with the equilateral triangle with sides of length 1, an inverted equilateral triangle with sides of length 1/2 is removed. Then, three inverted equilateral triangles with sides of length 1/4 are removed from this figure (see figure). The process continues in this way. Let Tn be the total area of the removed triangles after stage n of the process. The area of an equilateral triangle with side length L is A = √3L²/4.

a. Find T₁ and T₂, the total area of the removed triangles after stages 1 and 2, respectively. 

b. Find T_n, for n = 1, 2, 3,  . . . .
c. Find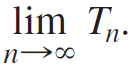

d. What is the area of the original triangle that remains as n →∞?

Transcribed Image Text:

lim Tn. п500 1 Second stage Initial stage First stage