The period of a pendulum is given by where is the length of the pendulum, g

The period of a pendulum is given by

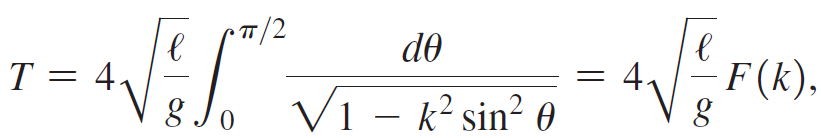
where ℓ is the length of the pendulum, g ≈ 9.8 m/s² is the acceleration due to gravity, k = sin (θ₀/2), and θ₀ is the initial angular displacement of the pendulum (in radians). The integral in this formula F(k) is called an elliptic integral, and it cannot be evaluated analytically.

a. Approximate F (0.1) by expanding the integrand in a Taylor (binomial) series and integrating term by term.

b. How many terms of the Taylor series do you suggest using to obtain an approximation to F(0.1) with an error less than 10^-3? 

c. Would you expect to use fewer or more terms (than in part (b)) to approximate F(0.2) to the same accuracy? Explain.

Transcribed Image Text:

•TT/2 do T = 4. gJ. F(k), Vi - k²sin² 0