There are several proofs of Taylor’s Theorem, which lead to various forms of the remainder. The following proof is instructive because it leads to two different forms of the remainder and it relies on the Fundamental Theorem of Calculus, integration by parts, and the Mean Value Theorem for Integrals. Assume that f has at least n + 1 continuous derivatives on an interval containing a.

a. Show that the Fundamental Theorem of Calculus can be written in the form

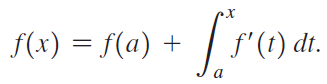
b. Use integration by parts (u = f'(t), dv = dt) to show that

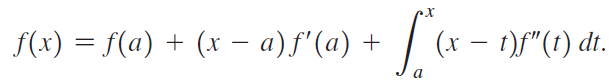
c. Show that n integrations by parts gives

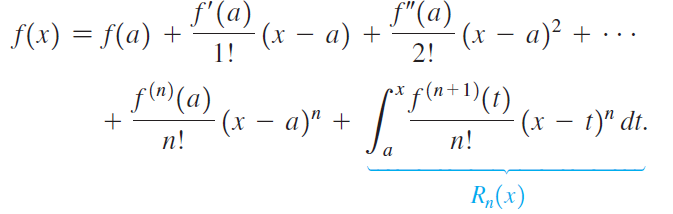
d. Challenge: The result in part (c) looks like f(x) = p_n(x) + R_n(x), where p_n is the nth-order Taylor polynomial and R_n is a new form of the remainder, known as the integral form of the remainder. Use the Mean Value Theorem for Integrals to show that R_n can be expressed in the form

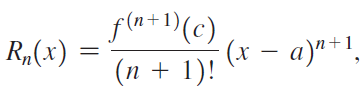
where c is between a and x.

Transcribed Image Text:

-Ггоя f'(t) dt. f(x) = f(a) + |