When approximating a function f using a Taylor polynomial, we use information about f and its derivatives at one point. An alternative approach (called interpolation) uses information about f at several different points. Suppose we wish to approximate f(x) = sin x on the interval [0, π].

a. Write the (quadratic) Taylor polynomial p₂ for f centered at π/2.

b. Now consider a quadratic interpolating polynomial q(x) = ax² + bx + c. The coefficients a, b, and c are chosen such that the following conditions are satisfied:

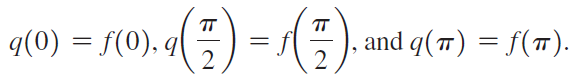
Show that

c. Graph f, p₂, and q on [0, π].

d. Find the error in approximating f(x) = sin x at the points π/4, π/2, π/4, and π using p₂ and q.

e. Which function, p₂ or q, is a better approximation to f on [0, π]? Explain.

() = (:. q(0) = f(0), q| and q(T) = f(T). 2