Exercises refer to the Laffer curve, originated by the economist Arthur Laffer. An idealized version of this curve is shown here. According to this curve, decreasing a tax rate, say from x₂ percent to x₁ percent on the graph, can actually lead to an increase in government revenue. The theory is that people will work harder and earn more money if they are taxed at a lower rate, so the government ends up with more revenue than it would at a higher tax rate. All economists agree on the endpoints—0 revenue at tax rates of both 0% and 100%—but there is much disagreement on the location of the tax rate x₁ that produces the maximum revenue.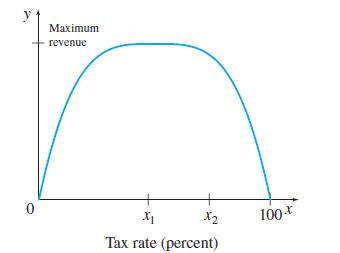

Find the equations of two quadratic functions that could describe the Laffer curve by having zeros at x = 0 and x = 100. Give the first a maximum of 100 and the second a maximum of 250, then multiply them together to get a new Laffer curve with a maximum of 25,000. Plot the resulting function.

Transcribed Image Text:

0 Maximum revenue x1 X2 Tax rate (percent) 100x