Mathematical models of ground temperature variation usually involve Fourier series or other sophisticated methods. However, the elementary
Question:
Mathematical models of ground temperature variation usually involve Fourier series or other sophisticated methods. However, the elementary model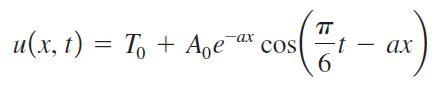
has been developed for temperature 0(x, t) at a given location at a variable time t (in months) and a variable depth x (in centimeters) beneath Earth’s surface, T0 is the annual average surface temperature, and A0 is the amplitude of the seasonal surface temperature variation. Assume that T0 = 16°C and A0 = 11°C at a certain location. Also assume that a = 0.00706 in cgs (centimeter-gram-second) units.
(a) At what minimum depth x is the amplitude of u(x, t) at most 1°C?
(b) Suppose we wish to construct a cellar to keep wine at a temperature between 14°C and 18°C. What minimum depth will accomplish this?
(c) At what minimum depth x does the ground temperature model predict that it will be winter when it is summer at the surface, and vice versa? That is, when will the phase shift correspond to 1/2 year?
(d) Show that the ground temperature model satisfies the heat equation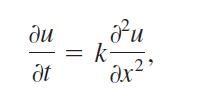
where k is a constant.
Step by Step Answer:
a The amplitude of xt is given by 11e 000706x We need to find where ...View the full answer
