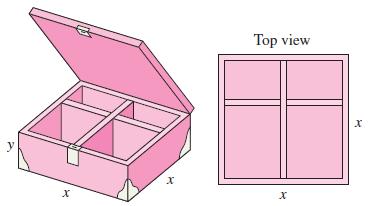
Suppose the jewelry box in Exercise 48 is designed so that the material in the top costs twice as much as the material in the bottom and sides and three times as much as the material in the interior partitions. What dimensions minimize the total cost of constructing the box?

Data from Exercises 48

A jewelry box is constructed by partitioning a box with a square base as shown in the accompanying figure. If the box is designed to have volume 800 cm³, what dimensions should it have to minimize its total surface area (top, bottom, sides, and interior partitions)? Notice that we have said nothing about where the partitions are located. Does it matter?

Transcribed Image Text:

X Top view X X