Question: Assume independence, and let p ij = n ij /n and ÏÌ ij = p i+ p +j . a. Show that p ij and

Assume independence, and let pij= nij/n and π̂ij= pi+p+j.

a. Show that pij and π̂ij are unbiased for πij = πi+ π+j.

b. Show that var(pij) = Ï€i+ Ï€+j(1 €“ Ï€i+ Ï€+j)/n 

c. Using E(pi+ p+j)2 = E(p2i+) E(p2+j) and E(p2i+) = var (pi+) + [E(pi+)]2, show that

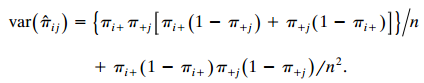
) = {T;+ T+[T;+ (1 – 7+;) + T +; (1 – T;+ var( î¡;) + π- (1- π.) π., (1- π.;)/n'.

) = {T;+ T+[T;+ (1 7+;) + T +; (1 T;+ var( ;) + - (1- .) ., (1- .;)/n'.

Step by Step Solution

★★★★★

3.41 Rating (154 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer
Step: 1 Unlock

a For multinomial sampling n ij has a binomial distribution with expectation n ij n i j Sin... View full answer

blur-text-image
Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock
Step: 3 Unlock

Students Have Also Explored These Related Categorical Data Analysis Questions!

Q:

Let Î²Ì M = log (p +1 p 2+ /p +2 p 1+ ) refer to marginal model (10.6) and Î²Ì C = log (n 21 /n 12 ) to conditional model (10.8). Using the delta method, show that...

Q:

Let Y i be bin(n i , Ï i ) at x i , and let p i = y i /n i . For binomial GLMs with logit link: a. For p i near Ï i , show that b. Show that z 1 (t) in (5.23) is a linearized version of the...

Q:

Let y i , i = 1,...,n, denote n independent binary random variables. a. Derive the log likelihood for the probit model Φ 1 [Ï(x i )] = j β j x ij . b. Show that the...

Q:

Exercises Chapter 2 2.1 Marginal and conditional probability: The social mobility data from Section 2.5 gives a joint probability distribution on (Y1 , Y2 )= (father's occupation, son's occupation)....

Q:

complete all using simple calculations 1 Consider the following two random samples of ten observations which come from the distributions of random variables which assume non-negative integer values...

Q:

(a) In SystemVerilog, what is the difference between: (i) The ternary operator ? and if...then...else statements? [2 marks] (ii) always_ff and always_comb? [2 marks] (iii) Blocking, non-blocking and...

Q:

BE562: Problem Set 3 Fall 2016 Due 10/21/2016 8PM 1. Hidden Markov Models and Protein Structure (20 pts) One biological application of hidden Markov models is to determine the secondary structure...

Q:

I need your help. This HM is due tomorrow at 4:00pm Spring 2016 - EBF 304W Homework 2 Due: 5:00pm on Friday, 12 February 2016 (via ANGEL) 50 points Instructions: Please answer all questions clearly...

Q:

Please someone answer my question, I will give thumbs up for the answer to my question! The program must be modified so it also prints the maximum profit path and prints the maximum profit and the...

Q:

In an I J contingency table, let ij denote local odds ratio (2.10), and let ij denote its sample value. a. show that asymp. cov(n log ij , n log i+1, j ) = [ 1 i+1, j + 1 i+1, j+1 ]. b. Show...

Q:

Year Peak Entertainment acquires its l00-percent-owned subsidiary Saddlestone Inc. on January 1, 2013. In preparing to consolidate Peak and Saddlestone at December 31, 2013, you assemble the...

Q:

Based on the data in Exercise 7-11 and assuming that cost was determined by the FIFO method, show how the merchandise inventory would appear on the balance sheet.

Q:

1. Which INT 21h function would you use to get the cluster size of a disk drive?

Q:

1.2.4 A fair coin is tossed until the first time that the same side appears twice in succession. Let N be the number of tosses required. (a) Determine the probability mass function for N. (b) Let A...

Q:

In Example 4, a random drawing was held to select the winners of the football tickets. Organizers randomly chose two numbers from a collection of slips of paper numbered 1 through 60. Using the Table...

Q:

Use the Random Numbers applet on the text CD or use software to (a) answer the previous exercise and (b) select a simple random sample of three students out of a class of 500 students.

Q:

Use the Random Numbers applet on the text CD to select 10 of the 60 school district accounts described in Example 5. Explain how you did this, and identify the accounts to be sampled.

Q:

You have just completed the first year of operation for your business and have the following information: sales, $200,000; cost of goods, $140,000; rent, $18,000; utilities, $8,400; insurance,...

Q:

Derek will deposit $1,789.00 per year into an account starting today and ending in year 21.00. The account that earns 8.00%. How much will be in the account 21.0 years from today? Attempts Remaining:...

Q:

Risky Business wants to know the payback period, NPV, IRR, MIRR, and Pl of this project. The appropriate discount rate for the project is 13%. If the cutoff period is 6 years for major projects,...