For Table 7.13, let Y = belief in life after death, x₁= gender (1 = females, 0 = males), and x₂= race (1 = whites, 0 = blacks). Table 7.14 shows the fit of the model  log(Ï€_j/Ï€₃) = α_j+ β_j^Gx₁+ β_j^Rx₂, j = 1, 2,

with SE values in parentheses.

Table 7.13:

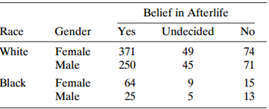
Table 7.14:

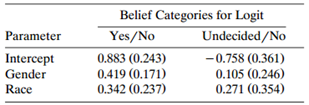
a. Find the prediction equation for log(Ï€₁/Ï€₂).

b. Using the yes and no response categories, interpret the conditional gender effect using a 95% confidence interval for an odds ratio.

c. Show that for white females, π̂₁ = PÌ‚(Y = yes) = 0.76.

d. For this fit, G² = 0.9. Explain why residual df = 2. Deleting the gender effect, G² = 8.0. Test whether opinion is independent of gender, given race. Interpret.

Belief in Afterlife Race Gender Yes Undecided No White Female Male 371 250 49 74 45 71 Black Female 64 9. 15 Male 25 13 Parameter Intercept Gender Belief Categories for Logit Yes/No 0.883 (0.243) 0.419 (0.171) 0.342 (0.237) Undecided/No -0.758 (0.361) 0.105 (0.246) 0.271 (0.354) Race