Question: For the toxicity study of Table 12.9, collapsing to a binary response, consider linear logit models for the probability a fetus is normal. a. Does

For the toxicity study of Table 12.9, collapsing to a binary response, consider linear logit models for the probability a fetus is normal.

a. Does the ordinary binomial model show evidence of overdispersion?

b. Fit the linear logit model using the quasi-likelihood approach with inflated binomial variance. How do the standard errors change?

c. Fit the linear logit model using quasi-likelihood with beta-binomial variance. Interpret and compare with previous results.

d. Fit the linear logit model using a GEE approach with exchangeable working correlation among fetuses in the same litter. Interpret and compare with previous results, including comparing the estimated GEE correlation with the estimate ?? from part (c).

e. Fit the linear logit GLMM after adding a litter-specific normal random effect. Interpret and compare with previous results.

Table 12.9:

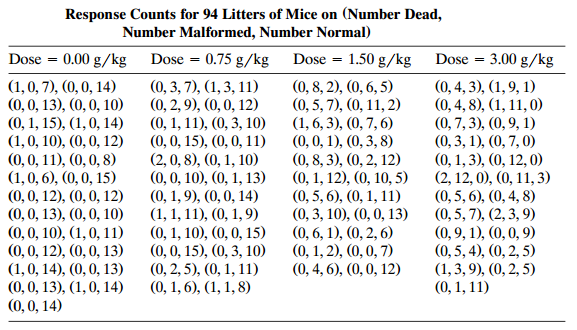
Response Counts for 94 Litters of Mice on (Number Dead, Number Malformed,

Response Counts for 94 Litters of Mice on (Number Dead, Number Malformed, Number Normal) Dose = 0.00 g/kg Dose = 3.00 g/kg Dose = 0.75 g/kg Dose = 1.50 g/kg (0, 3, 7), (1,3, 11) (0, 2, 9), (0,0, 12) (0, 1, 11), (0, 3, 10) (0, 0, 15), (0, 0, 11) (2, 0, 8), (0, 1, 10) (0, 0, 10), (0, 1, 13) (0, 1, 9), (0,0, 14) (1, 1, 11), (0, 1,9) (0, 1, 10), (0, 0, 15) (0, 0, 15), (0, 3, 10) (0, 2, 5), (0, 1, 11) (0, 1, 6), (1, 1, 8) (0, 8, 2), (0, 6, 5) (0, 5, 7), (0, 11, 2) (1, 6, 3), (0, 7, 6) (0, 0, 1), (0, 3, 8) (0, 8, 3), (0, 2, 12) (0, 1, 12), (0, 10, 5) (0, 5, 6), (0, 1, 11) (0, 3, 10), (0, 0, 13) (0, 6, 1), (0, 2, 6) (0, 1, 2), (0,0, 7) (0, 4, 6), (0, 0, 12) (1,0, 7), (0, 0, 14) (0, 0, 13), (0, 0, 10) (0, 1, 15), (1,0, 14) (1,0, 10), (0, 0, 12) (0, 0, 11), (0, 0, 8) (1,0, 6), (0, 0, 15) (0, 0, 12), (0, 0, 12) (0, 0, 13), (0, 0, 10) (0, 0, 10), (1,0, 11) (0, 0, 12), (0, 0, 13) (1,0, 14), (0,0, 13) (0, 0, 13), (1,0, 14) (0, 0, 14) (0, 4, 3), (1,9, 1) (0, 4, 8), (1, 11, 0) (0, 7, 3), (0, 9, 1) (0, 3, 1), (0, 7, 0) (0, 1, 3), (0, 12, 0) (2, 12, 0), (0, 11, 3) (0, 5, 6), (0, 4, 8) (0, 5, 7), (2, 3, 9) (0, 9, 1), (0, 0, 9) (0, 5, 4), (0, 2, 5) (1,3, 9), (0, 2, 5) (0, 1, 11)

Step by Step Solution

★★★★★

3.39 Rating (168 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

a Yes the ordinary bin omial model shows evidence of over dis p ersion b The standard errors change ... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Categorical Data Analysis Questions!

The hypothetical data below are from a toxicity study designed to measure the effectiveness of different doses of a pesticide on mosquitoes. The table below summarizes the concentration of the...

The following data are from Gennings, Chinchilli, and Carter, (1989). An in vitro toxicity study of isolated hepatocyte suspensions was conducted to study the impact of combining carbon tetrachloride...

Refer to Exercise 18.30. In Exercise 18.30 The following data are from Gennings, Chinchilli, and Carter, (1989). An in vitro toxicity study of isolated hepatocyte suspensions was conducted to study...

10.19 Refer to the toxicity study with data summarized in Table 10.12. Collapsing the ordinal response to binary in terms of whether with data summarized in the outcome is normal, consider logistic...

Critical review of the Reading Summary of the reading Critical evaluation of the reading It is tempting to assume that climate change equally influences the lives of women and men because the most...

Name : BIST 512 : Categorical Data Analysis Final Exam May 9th, 2pm to 4:30pm There are seven problems. Read all problems carefully before starting. Put your name on every sheet of paper before you...

Center for Learning and Technology COURSE SYLLABUS PRINCIPLES OF STATISTICS STA-201-GS Course Syllabus PRINCIPLES OF STATISTICS STA-201-GS Thomas Edison State College May 2015 Course Essentials...

Supply Chain Management Introduction Outline What is supply chain management? Significance of supply chain management. Push vs. Pull processes utdallas.edu/~metin 1 A Generic Supply Chain Sources:...

Exercises Chapter 2 2.1 Marginal and conditional probability: The social mobility data from Section 2.5 gives a joint probability distribution on (Y1 , Y2 )= (father's occupation, son's occupation)....

1. Calculate the sample size needed given these factors: one-tailed t-test with two independent groups of equal size small effect size (see Piasta, S.B., & Justice, L.M., 2010) alpha =.05 beta = .2...

Consider each of the following transactions. For each one, indicate whether it is a capital expenditure (C) or an expense in the current year (E). 1. Paid a consultant to advise on marketing strategy...

Stan is going to open a cupcake shop called Stan's Cupcakery in Montana. He found a great location that rents for only $5,810 per month. He will need to pay $24,527 to buy tables and chairs and all...

What is the most common funding sequence entrepreneurs typically use for new ventures? Bootstrapping to debt to equity Debt to bootstrapping to equity Debt to equity to bootstrapping Equity to...

7. Let us say we have three classification algorithms. How can we order these three from best to worst?

The GSS asks, What is the ideal number of kids for a family? When we use a recent GSS to evaluate how the mean response depends on gender and race (black or white), we get the results shown in the...

Refer to the previous exercise. Let f = 1 for females and 0 for males, and let r = 1 for blacks and 0 for whites. The regression model for predicting y = ideal number of kids is = 2.42 + 0.04f +...

For the FL Student Survey data file on the text CD, we use as the response variable sports (the number of weekly hours engaged in sports and other physical exercise). For the explanatory variables,...

Here is the link for texmessages.rds dataset. Please comment below if you have problems accessing it. please help me with the solution and rcode....

Choose the correct response(s) i. For bonds selling at par (face) value, the price of the bond is equal to the face value of the bond. ii. For bonds selling at a discount, the bond's yield is greater...

Happy Books sells paperback books for $7 each. The variable cost per book is $5. At current annual sales of 200,000 books, the publisher is just breaking even. It is estimated that if the authors'...