Refer to Problem 11.2. Further study shows evidence of an interaction between gender and substance type. Using GEE with exchangeable working correlation, the model fit for the probability π of using a particular substance is

logit(π̂) = €“ 0.57 + 1.93S₁ + 0.86S₂ + 0.38R €“ 0.20G + 0.37G × S₁ + 0.22G × S₂,

where R, G, S₁, S₂ are dummy variables for race (1 = white), gender (1 = female), and substance type (S₁ = 1, S₂ = 0 for alcohol; S₁ = 0, S₂ = 1 for cigarettes; S₁ = S₂ = 0 for marijuana). Show that:

a. The estimated odds a nonwhite male has used marijuana are exp( €“ 0.57) = 0.57.

b. Given gender, the estimated odds a white subject used a given substance are 1.46 times the estimated odds for a black subject.

c. Given race, the estimated odds a female has used alcohol are 1.19 times the estimated odds for males; for cigarettes and for marijuana, the estimated odds ratios are 1.02 and 0.82.

d. Given race, the estimated odds a female has used alcohol (cigarettes) are 9.97 (2.94) times the estimated odds she has used marijuana.

e. Given race, the estimated odds a male has used alcohol (cigarettes) are 6.89 (2.36) times the estimated odds he has used marijuana. Interpret the interaction.

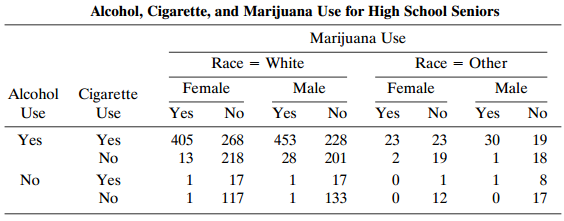
Data from Prob. 11.2:

Refer to Table 9.1. Fit a marginal model to describe main effects of race, gender, and substance type (marijuana, alcohol, cigarettes) on whether a subject had used that substance. Summarize effects.

Table 9.1:

Transcribed Image Text:

Alcohol, Cigarette, and Marijuana Use for High School Seniors Marijuana Use Race = White Female Race = Other Male Yes Male Female Alcohol Cigarette Yes Yes No Yes No No Use Use No Yes Yes 405 13 228 23 30 19 18 453 23 268 218 19 2 No 28 201 17 133 No Yes 1 17 1. 117 12 17 No