In Illustration 3.4-6 we considered the compression of an ideal gas in which P V^⋎ = constant, where ⋎  = C^∗_P/C^∗_V. Show that such a pressure-volume relationship is obtained in the adiabatic compression of an ideal gas of constant heat capacity.

Illustration 3.4-6

Showing That the Change in State Variables between Fixed Initial and Final States Is Independent of the Path Followed 

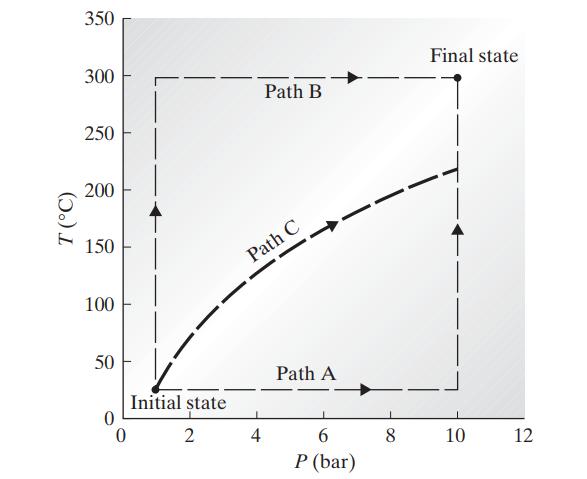
It is possible to go from a given initial equilibrium state of a system to a given final equilibrium state by a number of different paths, involving different intermediate states and different amounts of heat and work. Since the internal energy of a system is a state property, its change between any two states must be independent of the path chosen (see Sec. 1.3). The heat and work flows are, however, path-dependent quantities and can differ on different paths between given initial and final states. This assertion is established here by example. One mole of a gas at a temperature of 25°C and a pressure of 1 bar (the initial state) is to be heated and compressed in a frictionless piston and cylinder to 300°C and 10 bar (the final state). Compute the heat and work required along each of the following paths.

Path A. Isothermal (constant temperature) compression to 10 bar, and then isobaric (constant pressure) heating to 300°C 

Path B. Isobaric heating to 300°C followed by isothermal compression to 10 bar 

Path C. A compression in which P V^γ = constant, where γ = C^∗_P/C^∗_V, followed by an isobaric cooling or heating, if necessary, to 300°C.

For simplicity, the gas is assumed to be ideal with C^∗_P = 38 J/(mol K).

Transcribed Image Text:

(J.) I 350 300 250 200 150 100 50 0 1 P HI 0 Initial state 2 Path B Path C 4 Path A 6 P (bar) 8 Final state 10 12