\(1.5 \mathrm{kmol}\) of feed one that is \(40.0 \mathrm{~mol} \%\) methanol and \(60.0 \mathrm{~mol} \%\) water and \(1.0 \mathrm{kmol}\) of feed two that is \(20.0 \mathrm{~mol} \%\) methanol and \(80.0 \mathrm{~mol} \%\) water will be processed in a simple batch distillation. The following three approaches have been proposed:

a. Mix the two feeds together, and do the batch distillation.

b. Do a batch distillation of feed one until the still pot concentration is \(20 \mathrm{~mol} \%\) methanol (same as feed two), add feed two, and then complete the batch distillation.

c. Do a batch distillation of feed one and a separate batch distillation of feed two. Add the two distillate products and the two still-pot products.
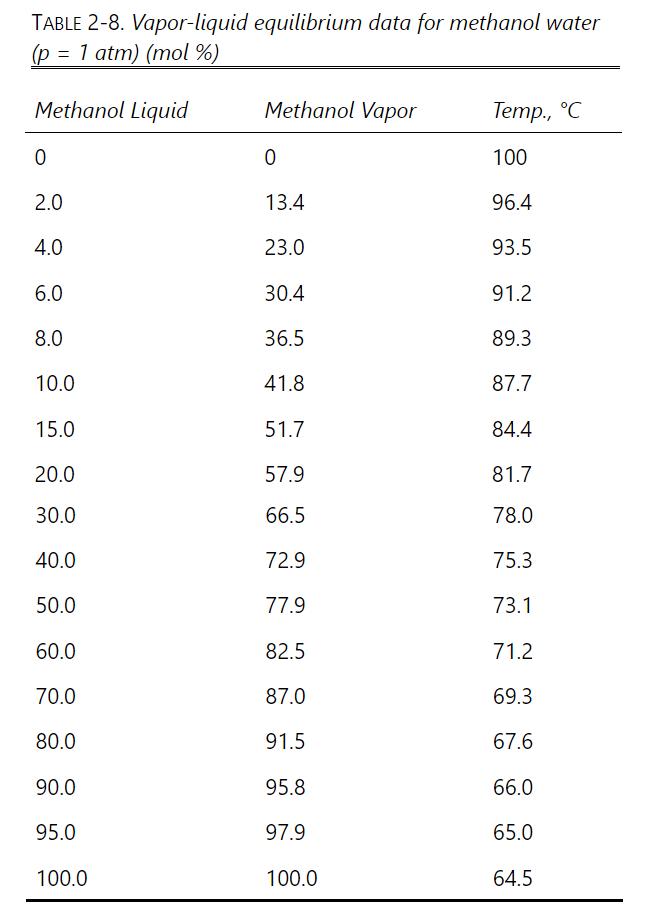
If we want \(\mathrm{x}_{\mathrm{W}, \text { fin }}=0.10\), do calculations for each method. Determine \(\mathrm{W}_{\text {final }}, \mathrm{D}_{\text {total }}\), and \(\mathrm{x}_{\mathrm{D}, \text { avg }}\), and compare the three methods. Equilibrium data are in Table 2-8. Logically, parts \(\mathrm{b}\) and \(\mathrm{c}\) should give the same result. If they do not, there is probably a numerical error from the use of Simpson's rule. Try dividing an area into two parts for more accuracy or use the Gaussian quadrature formula.

Table 2-8

Transcribed Image Text:

0 TABLE 2-8. Vapor-liquid equilibrium data for methanol water (p = 1 atm) (mol %) Methanol Liquid 0 Methanol Vapor Temp., C 100 2.0 13.4 96.4 4.0 23.0 93.5 6.0 30.4 91.2 8.0 36.5 89.3 10.0 41.8 87.7 15.0 51.7 84.4 20.0 57.9 81.7 30.0 66.5 78.0 40.0 72.9 75.3 50.0 77.9 73.1 60.0 82.5 71.2 70.0 87.0 69.3 80.0 91.5 67.6 90.0 95.8 66.0 95.0 97.9 65.0 100.0 100.0 64.5