Diffusion of a component A from a line source in a linear dimension x in an infinite medium as shown in Fig. P.12.8 is described by the following equation and boundary conditions:

FIGURE P.12.8:

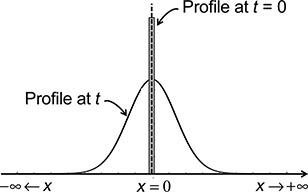
where  is the amount of A initially at x = 0 in mol per cm² of surface-perpendicular to x and  is the Dirac delta function.

(a) Obtain an analytical solution of this equation and boundary conditions. Use of the Laplace transform is recommended.

(b) Compare quantitatively your solution with the results of the simulation of random walk obtained in Problem P.10.1.

Data From Problem P.10.1:

A component A spreads from a point source as a result of Brownian motion in one dimension. At time t = 0, all molecules are located at x = 0.
During a 0.5 s time step, each molecule has the same probability of jumping a distance of 1.0 cm in either the positive or the negative x direction or to stay put. After 0.5 s, the process is repeated with each molecule having the same probability of traveling for another 0.5 s at the same speed in either positive or negative direction. Consider 1,000 molecules starting at x = 0 and plot their distribution as a function of distance from the source after 25, 50, 100, and 200 s, which correspond to 50, 100, 200, and 400 time steps, respectively

Profile at t- -00-x X=0 Profile at t=0 X+o