In inverted batch distillation (Diwekar, 1995; Robinson and Gilliland, 1950; Sorensen, 2014) the charge of feed is placed in the accumulator at the top of the column (Figure 9-9). Liquid is fed to the top of the column. At the bottom of the column, bottoms are continuously withdrawn, and part of the stream is sent to a total reboiler, vaporized, and sent back up the column. During the course of the batch distillation, the less volatile component (LVC) is slowly removed from the liquid in the accumulator, and the mole fraction MVC \(\mathrm{x}_{\mathrm{D}}\) increases. Assuming that holdup in the total reboiler, the total condenser, and the trays is small compared to the holdup in the accumulator, the Rayleigh equation for inverted batch distillation is

\[ \ln \left(D_{\text {final }} / F\right)=-_{x f e e d} \int^{x D, \text { final }}\left[\left(\mathrm{dx}_{D}\right) /\left(\mathrm{x}_{\mathrm{D}}-\mathrm{x}_{\mathrm{B}}\right)\right] \]

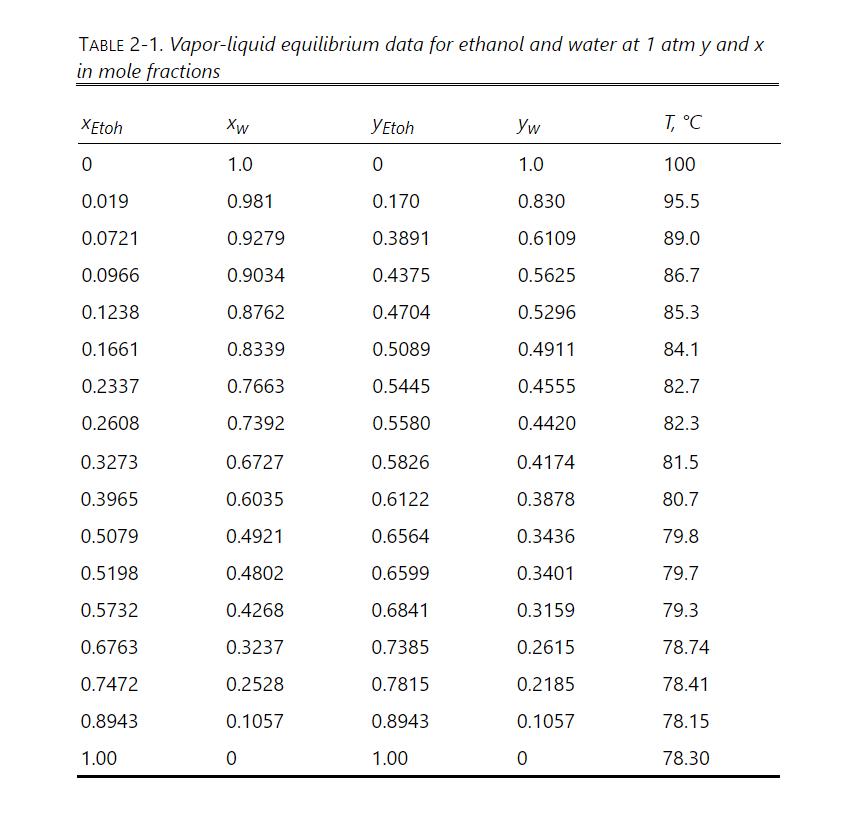
We feed the inverted batch system shown in Figure 9-9 with \(\mathrm{F}=10.0\) mole of a feed that is \(50.0 \mathrm{~mol} \%\) ethanol and \(50.0 \mathrm{~mol} \%\) water. We desire a final distillate mole fraction of 0.63 . There are two equilibrium stages in the column. The total reboiler, the total condenser, and the accumulator are not equilibrium contacts. VLE data are in Table 2-1. Find \(\mathrm{D}_{\text {final }}, \mathrm{B}_{\text {total }}\), and \(\mathrm{x}_{\mathrm{B}, \text { avg }}\) if the boilup ratio is 1.0 .

Figure 9-9

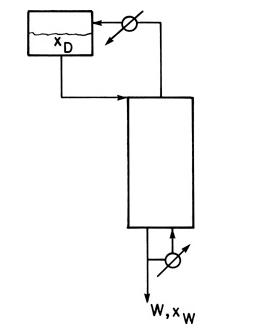
Table 2-1

Transcribed Image Text:

XD W,xw