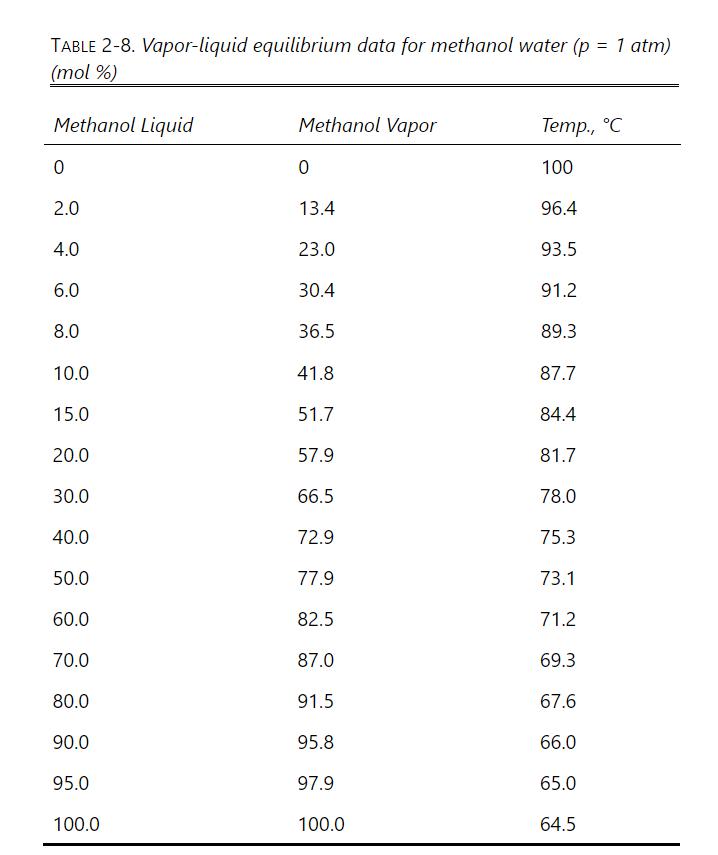
A nonvolatile solute is dissolved in \(1.0 \mathrm{kmol}\) of methanol. We wish to switch the solvent to water. Because the solution is already concentrated, a first batch distillation to concentrate the solution is not required. We desire to have the solute in \(1.0 \mathrm{kmol}\) of solution that is \(99.0 \mathrm{~mol} \%\) water and \(1.0 \mathrm{~mol} \%\) methanol. This can be done either with a constant-mole batch distillation or by diluting the mixture with water and then doing a simple batch distillation. VLE data (ignore the effect of the solute) are in Table 2-8. Dilute the original pure methanol (plus solute) with water and then do a simple batch distillation with the goal of having \(\mathrm{W}_{\text {fin }}=1.0\) and \(\mathrm{x}_{\mathrm{M}, \text { fin }}=0.01\). Find the moles of water added and the moles of water evaporated during the batch distillation. Compare with the constant-mole batch distillation in Problem 9.D17.

Problem 9.D17.

A nonvolatile solute is dissolved in \(1.0 \mathrm{kmol}\) of methanol. We wish to have the solute in \(1.0 \mathrm{kmol}\) of solution that is \(99.0 \mathrm{~mol} \%\) water and 1.0 \(\mathrm{mol} \%\) methanol. Because the solution is already concentrated, a first batch distillation to concentrate the solution is not required. VLE data (ignore the effect of the nonvolatile solute) are in Table 2-8. Do a constant-mole batch distillation from \(\mathrm{x}_{\mathrm{M}, \text { initial }}=1.0\) (pure methanol) to \(\mathrm{x}_{\mathrm{M}, \text { fin }}=0.01\). Find \(\mathrm{S}\), the moles of water evaporated with the methanol in the distillate, the kmol of distillate, and the methanol mole fraction in the distillate. Results can be compared with dilution followed by simple batch distillation in Problem 9.E4.

Table 2-8

Problem 9-E1

Because \(\mathrm{x}_{\mathrm{M}, \text { fin }}=0.01\) is quite small \((1 / \mathrm{y}=100\) at this limit), Simpson's rule is not accurate. Use the Gaussian quadrature formula instead.

Transcribed Image Text:

TABLE 2-8. Vapor-liquid equilibrium data for methanol water (p = 1 atm) (mol %) Methanol Liquid Methanol Vapor Temp., C 0 0 100 2.0 13.4 96.4 4.0 23.0 93.5 6.0 30.4 91.2 8.0 36.5 89.3 10.0 41.8 87.7 15.0 51.7 84.4 20.0 57.9 81.7 30.0 66.5 78.0 40.0 72.9 75.3 50.0 77.9 73.1 60.0 82.5 71.2 70.0 87.0 69.3 80.0 91.5 67.6 90.0 95.8 66.0 95.0 97.9 65.0 100.0 100.0 64.5