A simple batch distillation is used to process \(1.0 \mathrm{kmol}\) of methanol-water feed into three distillate fractions and a waste. The initial feed has \(\mathrm{x}_{F, \mathrm{M}}=\) 0.50 mole fraction. We want the average mole fractions of methanol in the distillate fractions to be \(\mathrm{x}_{\mathrm{D}, \text { avg, } 1}=0.70, \mathrm{x}_{\mathrm{D}, \text { avg, } 2}=0.60\), and \(\mathrm{x}_{\mathrm{D}, \text { avg, } 3}=0.40\). Equilibrium data are in Table 2-8.

Table 2-8

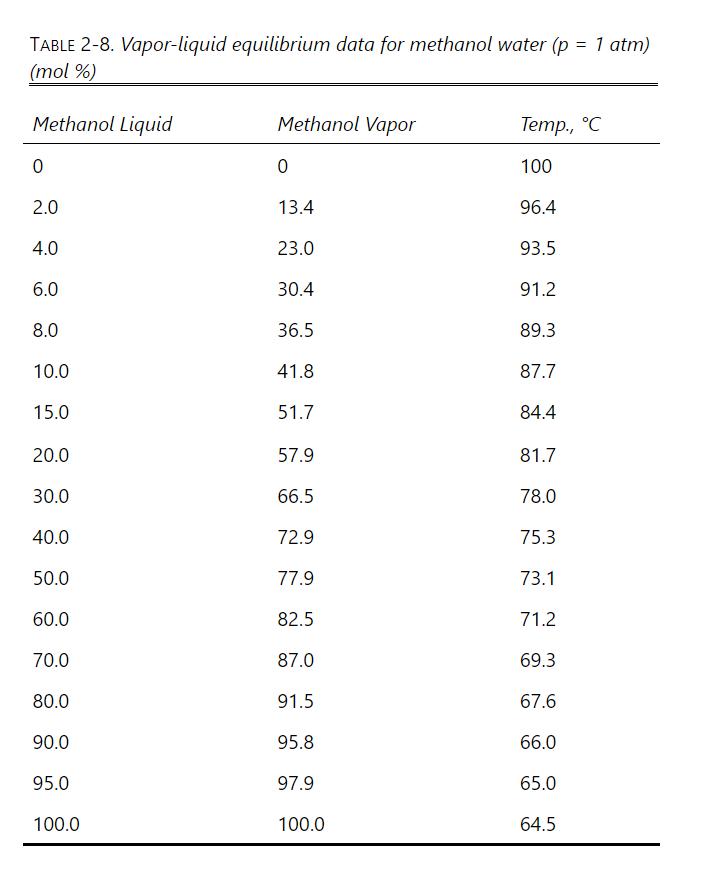
a. Find \(\mathrm{W}_{1, \text { fin }}, \mathrm{D}_{\mathrm{tot}, 1}, \mathrm{x}_{\mathrm{W}, \text { fin }, 1} ; \mathrm{W}_{2, \text { fin }}, \mathrm{D}_{\mathrm{tot}, 2}, \mathrm{x}_{\mathrm{Wfin}, 2} ;\) and \(\mathrm{W}_{3, \text { fin }}, \mathrm{D}_{\mathrm{tot}, 3}\), \(\mathrm{x}_{\mathrm{W}, \text { fin, } 3} \cdot\)

To make this problem tractable, the following procedure is suggested: Calculate relative volatility values \(\alpha_{M-\text { Water }}=\frac{y_{M} / x_{M}}{\left(1-y_{M}\right) /\left(1-x_{M}\right)}\) from equilibrium data at \(\mathrm{x}_{\mathrm{M}}=0.5,0.4,0.3,0.2,0.15\), and 0.10 . Over the different ranges of still pot mole fractions expected, calculate geometric average \(\alpha_{-}=\left(\alpha_{1} \alpha_{2} \ldots \alpha_{n}\right)^{1 / n}\) for each range.

Solve Eq. (9-13) on a spreadsheet to calculate \(\mathrm{W}_{\text {fin }}\) using the guessed value of \(\mathrm{x}_{\mathrm{W}, \text { final }}\). Calculate \(\mathrm{x}_{\mathrm{D}, \text { avg }}\) for each fraction. Use Goal Seek or Solver to find the value of \(\mathrm{x}_{\mathrm{W} \text {,fin }}\). If the average value of relative volatility used was for an obviously incorrect range, insert a corrected \(\alpha_{-}\), and repeat. Do this for each fraction.

Equation 9-13

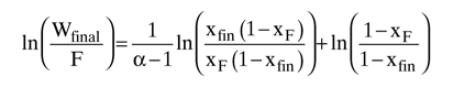
b. In the lab or plant, it is easier to collect fractions based on weight or time than based on mole fraction measurements. If heating is done at a rate of \(20 \mathrm{~kW}\), at what time in minutes should we switch from collecting the first fraction to collecting the second fraction? Required data are available in Appendix D in the back of book.

TABLE 2-8. Vapor-liquid equilibrium data for methanol water (p = 1 atm) (mol %) Methanol Liquid Methanol Vapor Temp., C 0 0 100 2.0 13.4 96.4 4.0 23.0 93.5 6.0 30.4 91.2 8.0 36.5 89.3 10.0 41.8 87.7 15.0 51.7 84.4 20.0 57.9 81.7 30.0 66.5 78.0 40.0 72.9 75.3 50.0 77.9 73.1 60.0 82.5 71.2 70.0 87.0 69.3 80.0 91.5 67.6 90.0 95.8 66.0 95.0 97.9 65.0 100.0 100.0 64.5