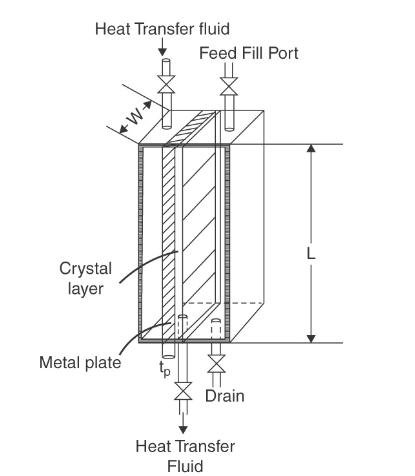
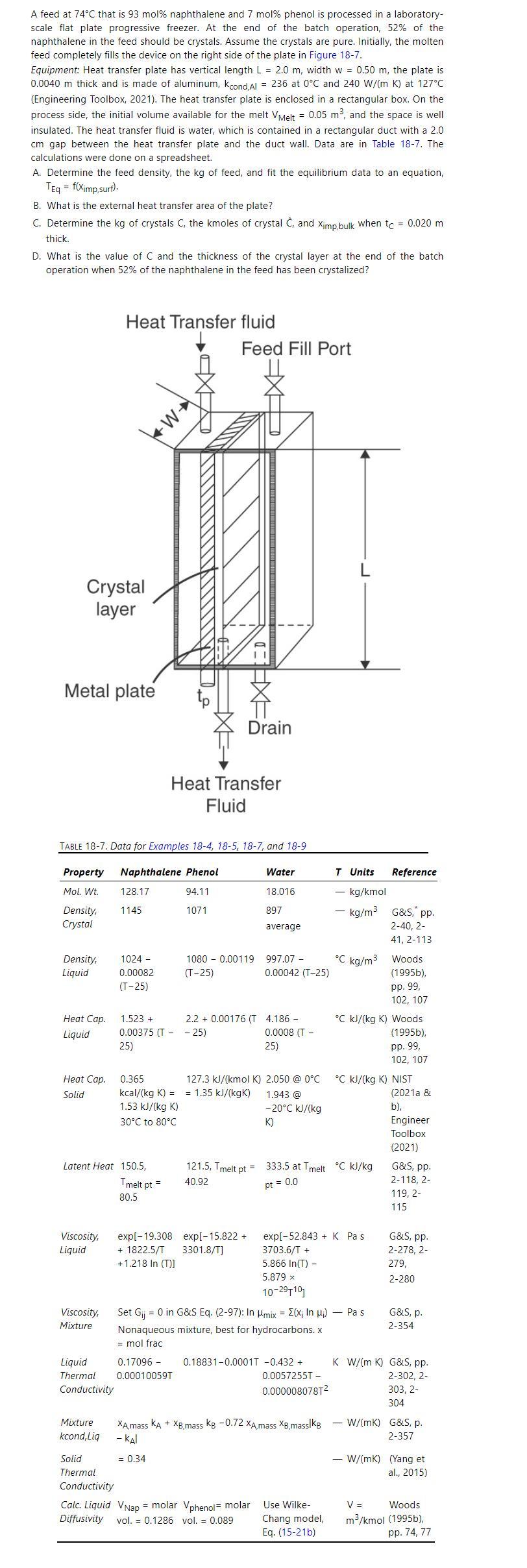
The size of the shell on the feed side of the flat plate static heat exchanger in Figure 18-7 controls the volume of feed, which sets the amount of feed. For the same recovery of product, the thickness of the crystal layer will be reduced if the shell size (and hence shell volume) are reduced. Of course, the amount of product per batch is reduced. Repeat the run in Examples 18-4 and 18-5 with \(52 \%\) recovery of naphthalene but with a shell that is spaced \(0.025 \mathrm{~m}\) on the process side.

a. Determine the \(\mathrm{kg}\) of feed.

b. Determine the \(\mathrm{kg}\) of crystals \(\mathrm{C}\), the kmoles of crystal \(\hat{\mathrm{C}}\), and \(\mathrm{x}_{\mathrm{imp}, \text { bulk }}\) when \(\mathrm{t}_{\mathrm{C}}=\) \(0.010 \mathrm{~m}\).

c. What is the value of \(\mathrm{C}\) and the thickness of the crystal layer at the end of the batch operation when \(52 \%\) of the naphthalene in the feed has been crystalized?

d. Start with \(\mathrm{t}_{\mathrm{C}}=0.009 \mathrm{~m}\) thick and find the time required to go to \(\mathrm{t}_{\mathrm{C}}=0.011 \mathrm{~m}\) thick. Operate with \(\mathrm{T}_{\mathrm{C}}=65^{\circ} \mathrm{C}\) and \(\left(\mathrm{T}_{\text {melt }}-\mathrm{T}_{\mathrm{C}}\right)=5^{\circ} \mathrm{C}\). Assume the crystals are pure, \(\mathrm{x}_{\text {imp }}=\) \(\mathrm{x}_{\text {phenol }}=0\). Use average conditions at \(\mathrm{t}_{\mathrm{C}}=0.010 \mathrm{~m}\).

Figure 18-7

Example 18-4

Example 18-5

Transcribed Image Text:

Crystal layer Heat Transfer fluid Feed Fill Port W+ D Metal plate Drain Heat Transfer Fluid L