Question:
Do the heat transfer calculation for a clean heat exchanger \(\left(t_{C}=0\right.\) and no crystal formation) in a natural convection progressive freezing device (see Figure 18-7) with the same dimensions as in Example 18-4. However, the temperatures are different. The temperature difference is \(\left(\mathrm{T}_{\text {melt }}-\mathrm{T}_{\mathrm{C}}\right)=0.2^{\circ} \mathrm{C}\), and the cold temperature is \(\mathrm{T}_{\mathrm{C}}=76.8^{\circ} \mathrm{C}\). The impurity (phenol) mole fraction is 0.07 and does not change because there is no driving force for mass transfer. You need to calculate properties at the new temperatures. This problem explores heat transfer after the progressive freezing device has been loaded and the melt plus crystallizer hardware are being cooled down but the melt temperature is still above the equilibrium temperature. Because there is no crystal layer, there is no need to calculate \(\mathrm{T}_{\text {Cry }}\), but you need to calculate \(\mathrm{T}_{\mathrm{P} 2}\). Report \(\mathrm{h}_{\text {Natt,convect }}\), \(h_{\text {transfer }}\), \(\mathrm{k}_{\text {cond }}\) /thickness, \(\mathrm{U}, \mathrm{T}_{\mathrm{p} 1}, \mathrm{~T}_{\mathrm{p} 2}, \mathrm{~T}_{\mathrm{Eq}}\), and Q. Data are in Tables 18-7 and 18-2 and Figure 18-1.
Example 18-4
Figure 18-1
Transcribed Image Text:
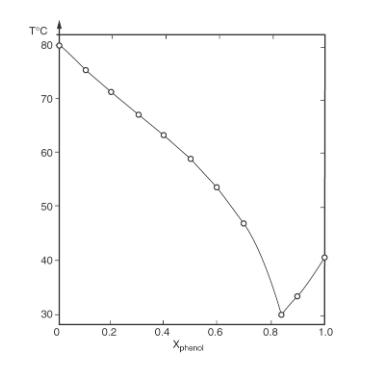
A feed at 74C that is 93 mol% naphthalene and 7 mol% phenol is processed in a laboratory- scale flat plate progressive freezer. At the end of the batch operation, 52% of the naphthalene in the feed should be crystals. Assume the crystals are pure. Initially, the molten feed completely fills the device on the right side of the plate in Figure 18-7. Equipment: Heat transfer plate has vertical length L = 2.0 m, width w = 0.50 m, the plate is 0.0040 m thick and is made of aluminum, kcond,Al = 236 at 0C and 240 W/(m K) at 127C (Engineering Toolbox, 2021). The heat transfer plate is enclosed in a rectangular box. On the process side, the initial volume available for the melt VMelt = 0.05 m, and the space is well insulated. The heat transfer fluid is water, which is contained in a rectangular duct with a 2.0 cm gap between the heat transfer plate and the duct wall. Data are in Table 18-7. The calculations were done on a spreadsheet. A. Determine the feed density, the kg of feed, and fit the equilibrium data to an equation, Teq = f(ximp,surf). B. What is the external heat transfer area of the plate? C. Determine the kg of crystals C, the kmoles of crystal , and Ximp,bulk when tc = 0.020 m thick. D. What is the value of C and the thickness of the crystal layer at the end of the batch operation when 52% of the naphthalene in the feed has been crystalized? Heat Transfer fluid Feed Fill Port Crystal layer W+ Metal plate Drain Heat Transfer Fluid Property TABLE 18-7. Data for Examples 18-4, 18-5, 18-7, and 18-9 Naphthalene Phenol Water T Units Reference Mol. Wt. 128.17 94.11 18.016 - kg/kmol Density, 1145 1071 897 - kg/m Crystal average G&S, pp. 2-40, 2- 41, 2-113 Density, 1024- Liquid 0.00082 (T-25) 1080 0.00119 (T-25) 997.07 - C kg/m Woods 0.00042 (T-25) (1995b), pp. 99, 102, 107 Heat Cap. 1.523+ 2.2 +0.00176 (T 4.186- C kJ/(kg K) Woods Liquid 0.00375 (T-25) 25) 0.0008 (T- 25) Heat Cap. Solid 0.365 kcal/(kg K) = 1.53 kJ/(kg K) 30C to 80C (1995b), pp. 99, 102, 107 127.3 kJ/(kmol K) 2.050 @ 0C = 1.35 kJ/(kgK) C kJ/(kg K) NIST 1.943 @ -20C kJ/(kg K) (2021a & b), Engineer Toolbox (2021) Latent Heat 150.5, Tmelt pt = 80.5 121.5, Tmelt pt 40.92 = 333.5 at Tmelt C kJ/kg pt = 0.0 G&S, pp. 2-118, 2- 119, 2- 115 Viscosity, Liquid exp[-19.308 + 1822.5/T +1.218 In (T)] exp[-15.822 + 3301.8/T] exp[-52.843 + K Pas 3703.6/T + 5.866 In(T) - G&S, pp. 2-278, 2- 5.879 * 279, 2-280 10-29T10 Viscosity, Mixture Set Gij = 0 in G&S Eq. (2-97): In mix = (x; In ;) - Pa s Nonaqueous mixture, best for hydrocarbons. x = mol frac 0.17096 - Thermal 0.00010059T Liquid G&S, P. 2-354 0.18831-0.0001 -0.432 + K W/(m K) G&S, pp. Conductivity 0.0057255T - 0.000008078T2 2-302, 2- 303, 2- 304 Mixture kcond,Liq XA mass KA + XB,mass kB -0.72 XA, mass XB,masslKB W/(mk) G&S, p. 2-357 Solid - KAI = 0.34 W/(mk) (Yang et al., 2015) Thermal Conductivity Calc. Liquid VNap = molar Vphenol molar Diffusivity vol. 0.1286 vol. = 0.089 Use Wilke- Chang model, Eq. (15-21b) V = Woods m/kmol (1995b), pp. 74, 77









