Scientists often find it helpful to use very simple expressions to estimate the order of magnitude of
Question:
Scientists often find it helpful to use very simple expressions to estimate the order of magnitude of a property without doing a detailed calculation. Treat a hydrogen atom as a one-dimensional box of length 150. pm (the approximate diameter of the atom) containing an electron and predict the wavelength of the radiation emitted when the electron falls to the lowest energy level from the next higher energy level.
ANTICIPATE Transitions in the hydrogen atom have wavelengths of the order of 100 nm, so expect a similar value.
PLAN The lowest energy level has n = 1, and so you can use Eq. 4 with n = 1 and m = me, the mass of the electron. The energy difference is carried away as a photon of radiation; so set the energy difference equal to hv and express v in terms of the corresponding wavelength by using Eq. 1 of Topic 1A (λ = c/v). The mass of the electron is given inside the back cover.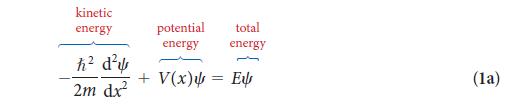
![]()
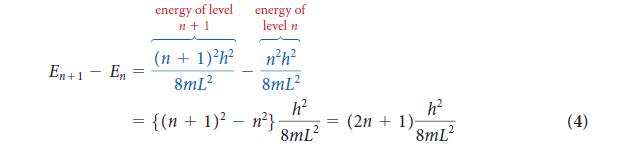
Step by Step Answer:

Chemical Principles The Quest For Insight
ISBN: 9781464183959
7th Edition
Authors: Peter Atkins, Loretta Jones, Leroy Laverman





