Question: Revisit Problem P16-3 where the RTD function is a hemicircle. The liquid-phase reaction is first order with k1 = 0.8 min 1 . What is

Revisit Problem P16-3 where the RTD function is a hemicircle. The liquid-phase reaction is first order with k1 = 0.8 min^–1. What is the conversion predicted by
a. The tanks-in-series model?
b. The dispersion model?

Problem P16-3

Consider the E(t) curve below.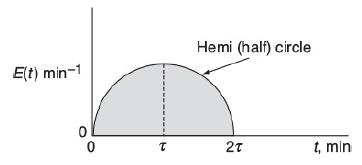 E(t) min-1 0 T Hemi (half) circle 20 t, min

A graph is shown, with t (in minutes) on horizontal axis and E of t (minutes inverse) on vertical axis. A hemi (half) circular curve starts at the origin and ends at 2 tau on the horizontal axis. It is symmetric about the vertical line at tau. Mathematically this hemi circle is described by these equations: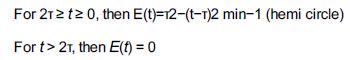 For 212 t 0, then For t> 21, then E(t) = 0 E(t)=12-(t-1)2 min-1 (hemi circle)

E(t) min-1 0 T Hemi (half) circle 20 t, min

Step by Step Solution

★★★★★

3.44 Rating (154 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

a b Closedclosed vessel dispersion model For a first ord... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Chemical Reaction Engineering Questions!

The Forest Service is deciding how to allocate its recreational funding. It can increase fishing opportunities in an area (for instance, by stocking), or it can build more hiking trails. It presents...

The following E(t) curves were obtained from a tracer test on two tubular reactors in which dispersion is believed to occur. A second-order reaction AkBwithkCA0=0.2 min1 is to be carried out in this...

The following additional information is available for the Dr. Ivan and Irene Incisor family from Chapters 1-5. Ivan's grandfather died and left a portfolio of municipal bonds. In 2012, they pay Ivan...

a. Example 17-2: Mean Conversion, Xseg, Calculations in a Real Reactor Wolfram and Python 1. How do C A0 , n and k affect the trajectories in X for the segregation model and the LFR? 2. Write a set...

a. Example 8-1: Trambouze Reactions Wolfram 1. Fix k 2 at 0.015 and then describe how the selectivity varies with k 1 and k 3 . 2. Write a conclusion about your experiments. Polymath 3. What would...

how to do this excell? 2.00 (50 pts) Revisit problem 2 of HW 5. Add the R2 to the non-linear regression done in HW5 and generate a residuals plot. Are the residuals randomly distributed around zero?...

how to do this in excell? 2.000 ( 50 pts) Revisit problem 2 of HW 5. Add the R2 to the non-linear regression done in HW5 and generate a residuals plot. Are the residuals randomly distributed around...

Revisit this problem ( look up the solution, it should be solved already ) : - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - You are designing the curriculum...

please answer these question due by 11:30 pm tonight QUESTION 4 5 points Based on the outcomes for the above processes which process would you recommend? (A, B or C) For the following tree: 50 Ship...

Its July 1, 20X2, and the market price of Warm Wayss common stock (Problem P16-3) is $175 per share. There are 1.1 million common shares outstanding, and the Retained earnings account shows a balance...

Your customers average order size is $2,601, with a standard deviation of $1,275. You are wondering what would happen if exactly 45 typical customers independently placed orders tomorrow. a.* Find...

If y=(x-1) log(x - 1)-(x + 1) log(x + 1), x then prove dy that = dx log x+1

5. Firms which have time as their competitive priority: (a) Deliver products at the earliest. (b) Deliver products well before the due date. (c) Deliver products as soon as they can after the due...

=+Specialized Semi- Navigational conductors Division Systems Division Sales: 640 units X $1,320 per unit $844,800 1,000 units X $1,984 per unit $1,984,000 Expenses: Variable: 640 units X $776 per...

How should we operate a mixed flow reactor so as to maximize the production of R? Separation and recycle of unused reactant is not practical. When aqueous A and aqueous B (C A0 = C B0 ) are brought...

How should we operate a mixed flow reactor so as to maximize the production of R? Separation and recycle of unused reactant is not practical. Under ultraviolet radiation, reactant A of C A0 = 10...

JAVA Using recursion, create a program that will allow for a user to enter 5 numbers. The program will provide the product of all 5 numbers using recursive methods.

Choose one of the security contexts you identified above that best includes as many elements of the system as drawn in the figure as possible. For this security context, state the success scenario...

Describe a strength and weakness of sensitivity analysis and scenario analysis..