Set up a stoichiometric table for each of the following reactions and express the concentration of each species in the reaction as a function of conversion, evaluating all constants (e.g., =, =). Next, assume the reaction follows an elementary rate law, and write the reaction rate solely as a function of conversion, that is, –r_A = f(X).
a. For the liquid-phase reaction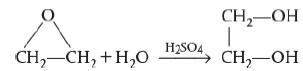

Ethylene oxide (C2H4O) reacts with water (H₂O) in the presence of sulfuric acid (H2SO4) as a catalyst to form ethylene glycol (C2H6O2).
the entering concentrations of ethylene oxide and water, after mixing the inlet streams, are 16.13 and 55.5 mol/dm3, respectively. The specific reaction rate is k = 0.1 dm³/mol · s at 300 K with E = 12500 cal/mol.
1. After finding –rA = f(X), calculate the CSTR space-time, τ, for 90% conversion at 300 K and also at 350 K.
2. If the volumetric flow rate is 200 liters per second, what are the corresponding reactor volumes?

b. For the isothermal gas-phase pyrolysis C₂H₆ → C₂H₄ = H₂ pure ethane enters a flow reactor at 6 atm and 1100 K, with ΔP = 0. Set up a stoichiometric table and then write –r_A = f(X). How would your equation for the concentration and reaction rate, that is, –r_A = f(X), change if the reaction were to be carried out in a constant-volume batch reactor?
c. For the isothermal, isobaric, catalytic gas-phase oxidation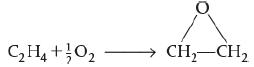

Ethylene (C2H4) reacts with half a molecule of oxygen (Half of O2) to form ethylene oxide (C2H4O).

the feed enters a PBR at 6 atm and 260°C, and is a stoichiometric mixture of only oxygen and ethylene. Set up a stoichiometric table and then write −r_A′ as a function of partial pressures. Express the partial pressures and −r_A′ as a function of conversion for (1) a fluidized batch reactor and (2) a PBR. Finally, write −r_A′
solely as a function of the rate constant and conversion.
d. Set up a stoichiometric table for the isothermal, catalytic gas-phase reaction carried out in a fluidized CSTR.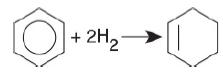

Benzene reacts with two molecules of hydrogen (2H2) to form cyclohexene.

A fluidized CSTR contains the fluidized catalyst pellets in it. It is cylindrical in the middle and funnel like at the top and the bottom ends.
The feed is stoichiometric and enters at 6 atm and 170°C. What catalyst weight is required to reach 80% conversion in a fluidized CSTR at 170°C and at 270°C?

The rate constant is defined with respect to benzene and υ₀ = 50 dm³/min. KB=53 molKgcat⋅min⋅atm3at 300 k with E=80 kJ/mol
First write the rate law in terms of partial pressures and then express the rate law as a function of conversion. Assume ΔP ≡ 0.

Transcribed Image Text:

CH,CH,+H,O HSO4 CH-OH T CH,-OH