The equations describing diffusion and reaction in porous catalysts also can be used to derive rates of
Question:
The equations describing diffusion and reaction in porous catalysts also can be used to derive rates of tissue growth and have been studied by Professor Kristi Anseth and her students at the University of Colorado. One important area of tissue growth is in cartilage tissue in joints such as the knee. Over 200,000 patients per year receive knee joint replacements. Alternative strategies include the growth of cartilage to repair the damaged knee. One approach is to deliver cartilage-forming cells in a hydrogel to the damaged area such as the one shown in Figure WP15-1.1 in additional material on the CRE Web site. Here, the patient’s own cells are obtained from a biopsy and embedded in a hydrogel, which is a cross-linked polymer network that is swollen in water.
In order for the cells to survive and grow new tissue, many properties of the gel must be tuned to allow diffusion of important species in and out (e.g., nutrients in and cell-secreted extracellular molecules such as collagen out). Because there is no blood flow through the cartilage, oxygen transport to the cartilage cells is primarily by diffusion. Consequently, the design must be such that the gel can maintain the necessary rates of diffusion of nutrients (e.g., O2) into the hydrogel. These rates of exchange in the gel depend on the geometry and the thickness of the gel. To illustrate the application of chemical reaction engineering principles to tissue engineering, we will examine
the diffusion and consumption of one of the nutrients, oxygen. Our examination of diffusion and reaction in catalyst pellets showed that in many cases the reactant concentration near the center of the particle was virtually zero. If this condition were to occur in a hydrogel, the cells at the center would die. Consequently, the gel thickness needs to be designed to allow rapid transport of oxygen.
Let’s consider the simple gel geometry shown in Figure P15-17B. We want to find the gel thickness at which the minimum oxygen consumption rate is 10–13 mol/cell/h (k=10−3 mol O2dm3h).
The cell density in the gel is 1010 cells/dm3, the bulk concentration of oxygen CA0 (z = 0) is 2 × 10–4 mol/dm3, and the diffusivity, DAB, is 10–5 cm2/s.
a. Show that the dimensionless form of concentration and length, ψ = CA/CA0, and λ = z/L, differential mole balance on O2 gives
d2ψdλ2−kL2DABCA0=0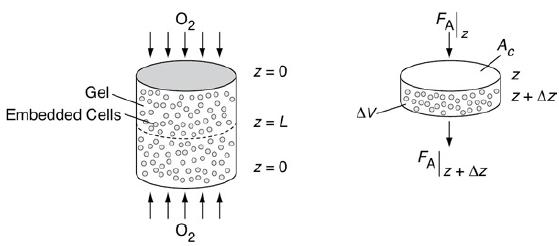
Schematic of cartilage cell system.
A cartilage cell system is shown in which embedded cells are present in the gel to which arrows are mapped in both directions. Z equals 0 is marked at the top and bottom and z equals L is marked at the middle of the cylinder. A cross-sectional area is shown. An arrow marked from top to bottom is marked F subscript A vertical bar z and the arrow coming out is marked F subscript A vertical bar z plus delta Z. The gel is marked delta V and the cross sectional surface is marked A subscript C.
b. Show the dimensionless O2 concentration profile in the gel is
ψ=CACA0=ϕ0λ(λ−2)+1
where
λ=z/Lϕ0=(k2DABCA0)L2
c. Solve the gel thickness when the concentration at z = 0 and CA = 0.1 mmole/dm3.
d. How would your answers change if the reaction kinetics were (1) first order in the O2 concentration with k1 = 10–2 h–1?
e. Carry out a quasi-steady-state analysis using Equation (WE15-1.19) from the Web site
(http://www.umich.edu/~elements/6e/15chap/expanded_ch15_tissue.pdf), along with the overall balance dNwdt=υcWO2|z=0Ac
to predict the O2 flux and collagen build-up as a function of time.
f. Sketch ψ versus λ at different times.
g. Sketch λc as a function of time.
Step by Step Answer:





