In chess, a knight can move in any direction, but it must move two spaces then turn and move one more space. The eight possible moves a knight can make from a given space are shown in the figure.

A graph in which each vertex represents a space on a five-by-six game board and each edge represents a move a knight could make is shown in the figure.

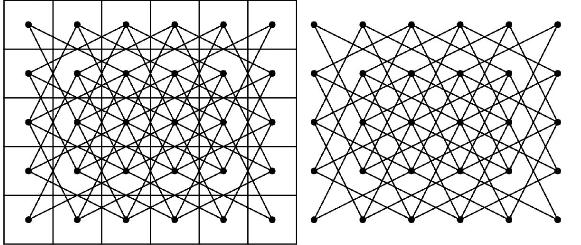
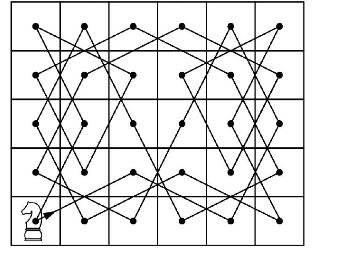
A knight's tour is a sequence of moves by a knight on a chessboard (of any size) such that the knight visits every square exactly once. If the knight's tour brings the knight back to its starting position on the board, it is called a closed knight's tour. Otherwise, it is called an open knight's tour. Determine if the closed knight's tour in the figure is most accurately described as a trail, a circuit, an Euler trail, or an Euler circuit of the graph of all possible knight moves. Explain your reasoning.

Transcribed Image Text:

2