What is the probability that the second punch is worth more than the first punch, given that the first punch was worth \(\$ 250\) ?

Deal with the game "Punch a Bunch," which appears on the TV game show The Price Is Right. In this game, contestants have a chance to punch through up to 4 paper circles on a board; behind each circle is a card with a dollar amount printed on it. There are 50 of these circles; the dollar amounts are given in this table:

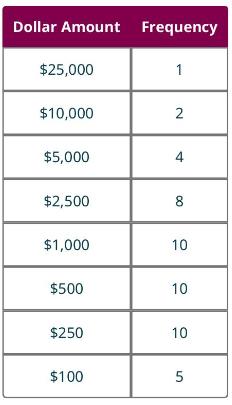
Contestants are shown their selected dollar amounts one at a time, in the order selected. After each is revealed, the contestant is given the option of taking that amount of money or throwing it away in favor of the next amount. (You can watch the game being played in the video Playing "Punch a Bunch." (https://openstax.org/r)
Playing_Punch_a_Bunch)) Jeremy is playing "Punch a Bunch" and gets 2 punches.

Transcribed Image Text:

Dollar Amount Frequency $25,000 1 $10,000 2 $5,000 4 $2,500 $1,000 00 8 10 10 $500 10 $250 10 10 $100 5