The Nyquist locus of a transfer function is given below:

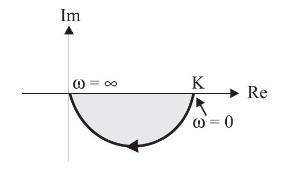
The locus is modified as shown below on addition of pole or poles to the original \(\mathrm{G}(\mathrm{s}) \mathrm{H}(\mathrm{s})\).

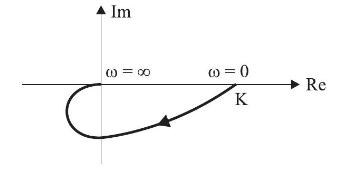
Then, the modified transfer function of the modified locus is
(a) \(\mathrm{G}(s) \mathrm{H}(\mathrm{s})=\frac{\mathrm{K}}{s\left(1+s \mathrm{~T}_{1}ight)}\)
(b) \(\mathrm{G}(s) \mathrm{H}(\mathrm{s})=\frac{\mathrm{K}}{\left(1+s \mathrm{~T}_{1}ight)\left(1+s \mathrm{~T}_{2}ight)}\)
(c) \(\mathrm{G}(s) \mathrm{H}(\mathrm{s})=\frac{\mathrm{K}}{s\left(1+s \mathrm{~T}_{1}ight)\left(1+s \mathrm{~T}_{2}ight)}\)
(d) \(\mathrm{G}(s) \mathrm{H}(s)=\frac{\mathrm{K}}{s\left(1+s \mathrm{~T}_{1}ight)\left(1+s \mathrm{~T}_{2}ight)\left(1+s \mathrm{~T}_{3}ight)}\)

Im (1) = K co=0 Re