A linear model of the -subsystem of a grid-connected converter (Mahmood, 2012) with a Y-Y transformer was

Question:

A linear model of the α-subsystem of a grid-connected converter (Mahmood, 2012) with a Y-Y transformer was presented as the plant in Problem 69 in Chapter 8. You were asked to find the transfer function of that plant, G_P(s) = V_α(s)/M_α(s).

a. Use the results of your solution to Problem 69, Chapter 8, to write the open-loop transfer function in pole-zero form with a unity gain. Then design a PID controller to yield a zero steady-state error for a step input with an overshoot of less than 10% and a natural frequency of 135.3.

b. Plot the time response, c(t), marking on it all relevant characteristics, such as the percent overshoot (if any), rise time, settling time, and final steady-state value. Also find all closed-loop poles of this system and the velocity error constant, Kv. Do you have any observations about the time response and/or the poles?

Data From Chapter 8 Problem 69:

A linear dynamic model of the α-subsystem of a gridconnected voltage source converter (VSC) using a Y-Y transformer is shown in Figure P8.20 (a) (Mahmood, 2012).

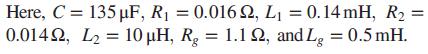
a. Find the transfer function G_P(s) = V_α(s)/M_α(s).

b. If G_P(s) is the plant in Figure P8.20(b) and GC(s) = K, use MATLAB to plot the root locus. On a closeup of the locus (from -300 to 0 on the real axis and from -50 to 5000 on the imaginary axis), find K and the coordinates of the dominant poles, which correspond to ζ = 0.012. Plot the output response, c(t) = v_α(t), at that value of the gain when a step input, r(t)= v_r (t)= 208 u(t) volts, is applied at t = 0. Mark on the time response graph, c(t), all relevant characteristics, such as the percent overshoot, peak time, rise time, settling time, and final steady-state value.