An inverted pendulum mounted on a motor-driven cart (Prasad, 2012) was the subject of Problem 33, Chapter

Question:

An inverted pendulum mounted on a motor-driven cart (Prasad, 2012) was the subject of Problem 33, Chapter 9. In that problem you were asked to develop Simulink models for two feed back systems, one of which was to control the cart position, x(t). At the recommended settings, the step response of that system was expected to satisfy the following requirements: a steady-state error, e(∞) < 2%, a peak time, T_P < 1.2 seconds, and a percent overshoot, %OS < 20.5%. Having concluded that the steady-state error was unacceptable, you designed a PID controller and found its recommended settings.

Digitize the Simulink model developed for PID control of the cart position in Part d of Problem 33, Chapter 9, by adding azero-order-holdsetto0.01second.Then, run a simulation to evaluate performance.

Data from Problem 33 Chapter 9

An inverted pendulum mounted on a motor-driven cart was introduced in Problem 30 in Chapter 3. Its state-space model was linearized around a stationary point, x₀ = 0 (Prasad, 2012). At the stationary point, the pendulum point-mass, m, is in the upright position at t = 0, and the force applied to the cart, u₀, is 0. Its model was then modified in Problem 55 in Chapter 6 to have two output variables: the pendulum angle relative to the y-axis, θ(t), and the horizontal position of the cart, x(t). MATLAB was then used to find its eigenvalues. Noting that only one pole (out of four) is located in the left half of the s-plane, we concluded that this unit requires stabilization.

Data from Problem 30 Chapter 3

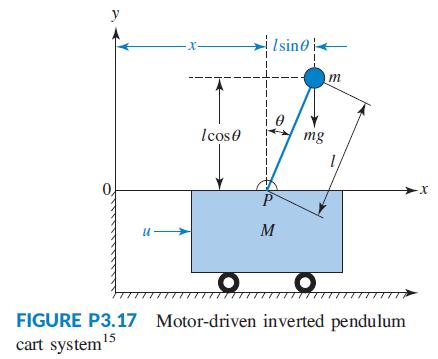
Figure P3.17 shows a free-body diagram of an inverted pendulum, mounted on a cart with a mass, M. The pendulum has a point mass, m, concentrated at the upper end of a rod with zero mass, a length, l, and a frictionless hinge. A motor drives the cart, applying a horizontal force, u(t). A gravity force, mg, acts on m at all times. The pendulum angle relative to the y-axis, θ, its angular speed, θ´ , the horizontal position of the cart, x, and its speed, x´, were selected to be the state variables.