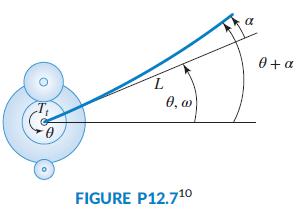
The study of the flexible links, such as the one shown in Figure P12.7, is important because of their application to the control of flexible lightweight robots (Saini, 2012). The flexible link angle is deflected by a servomotor. It is assumed that the base angle, θ(t), and the tip angular deflection relative to the unde formed link, α(t), can be measured. For a specific setup, a state-space model of the system was developed. The state vector is

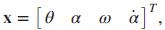
here ω(t) = θ(t) and input u(t) is the voltage applied to the servomotor. Thus the system is represented as ẋ = Ax + Bu, y = Cx where

It is desired to build state-feedback compensation around this system so that the system’s characteristic equation becomes D(s) = (s + 10)⁴. In order to do this:

a. Find the system’s controllability matrix C_MO and show that the system is controllable.

b. Find the original system’s characteristic equation and use it to find a phase-variable representation of the system.

c. Find the phase-variable system’s controllability matrix CMP and then find the transformation matrix P = C_MOC^-1_MP.

d. Use the phase-variable representation to find a feedback gain matrix K_P = [k_1p k_2p k_3p k_4p]  that will place the closed-loop poles in the desired positions.

e. Find the corresponding feedback gain matrix K_O = KP P-¹.

Transcribed Image Text:

x = [0 a à]".