We want to use an observer in a textile machine to estimate the state variables. The 2-input, 1-output systems model is = Ax +

We want to use an observer in a textile machine to estimate the state variables. The 2-input, 1-output system’s model is ẋ = Ax + Bu; y = Cx, where (Cardona, 2010)

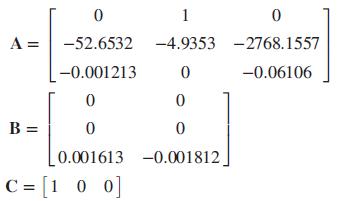
a. Find the system’s observability matrix O_Mz and show that the system is observable.

b. Find the original system’s characteristic equation and use it to find an observable canonical representation of the system.

c. Find the observable canonical system’s observability matrix O_Mx and then find the transformation matrix P = O^-1_Mz O_Mx.

d. Use the observable canonical representation to find an observer gain matrix L_x = [l_1x l_2x l_3x l_4x ]^T so that the observer characteristic polynomial is D(s) = s³ + 30s² + 316s + 1160.

e. Find the corresponding observer gain matrix L_z  = PL_x.

1 A = -52.6532 -4.9353 -2768.1557 -0.001213 -0.06106 B = 0.001613 -0.001812 C = [1 0 0]