The preceding material can be further explained by the following example. We keep our one-factor model here but make three specific assumptions:

1. All securities have the same expected return of 10 percent. This assumption implies that the first row of Equation 12.4 also must equal 10 percent because this row is a weighted average of the expected returns of the individual securities.

2. All securities have a beta of 1. The sum of the terms inside the parentheses in the second row of Equation 12.4 must equal 1 because these terms are a weighted average of the individual betas. Because the terms inside the parentheses are multiplied by F, the value of the second row is 1 × F = F .

3. In this example, we focus on the behavior of one individual, Walter V. Bagehot. Walter decides to hold an equally weighted portfolio. That is, the proportion of each security in his portfolio is 1 / N .

We can express the return on Walter’s portfolio as follows:

Return on Walter V. Bagehot’s Portfolio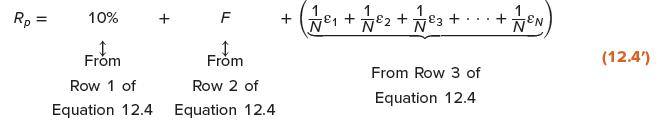

We mentioned before that as N increases without limit, Row 3 of Equation 12.4 becomes equal to zero.4 The return on Walter’s portfolio when the number of securities is very large is:

The key to diversification is exhibited in Equation 12.4″. The unsystematic risk of Row 3 vanishes while the systematic risk of Row 2 remains.

This is illustrated in Figure 12.2. Systematic risk, captured by variation in the factor F, is not reduced through diversification. Conversely, unsystematic risk diminishes as securities are added, vanishing as the number of securities becomes infinite. Our result is analogous to the diversification example of the previous chapter. In that chapter, we said that undiversifiable or systematic risk arises from positive covariances between securities. In this chapter, we say that systematic risk arises from a common factor, F. Because a common factor causes positive covariances, the arguments of the two chapters are parallel.

Figure 12.2 Diversification and the Portfolio Risk for an Equally Weighted Portfolio

Transcribed Image Text:

Rp = 10% From Row 1 of Equation 12.4 F From Row 2 of Equation 12.4 +₁ +₂ +₂ + ... From Row 3 of Equation 12.4 NEN (12.4')