A satellite control system is modeled as shown in Fig. P9.2-4. This system is described in Problem 1.4-1. For this problem, let $D\left(z\right)=1$. In addition, $K=1,T=1s,J=4$, and $H_k=1$. From the $z$-transform tables,

$$\frac{z-1}{z}z\left[\frac{1}{4s^3}\right]=\frac{0.125(z+1)}{(z-1{)}^2}$$

A state model for this system is given by

$$\begin{array}{c}x(k+1)=\left[\begin{array}{cc}1& 1\\ 0& 1\end{array}\right]x\left(k\right)+\left[\begin{array}{c}0.125\\ 0.25\end{array}\right]u\left(k\right)\\ y\left(k\right)=\left[\begin{array}{cc}1& 0\end{array}\right]x\left(k\right)\end{array}$$

where $x_1\left(k\right)$ is angular position and $x_2\left(k\right)$ is angular velocity.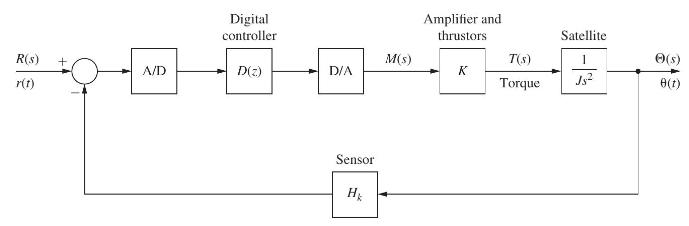

(a) Show that the closed-loop system is unstable.
(b) Using pole-placement design, find the gain matrix $K$ that yields the closed-loop damping ratio $\zeta =0.707$ and the time constant $\tau =4s$.

(c) Show that the gain matrix $K$ in part (b) yields the desired closed-loop characteristic equation, using (9-15).

Equation 9-15

Problem 1.4-1

Given that (11-21) and (11-22) are valid, derive (11-23).

Equation 11-21

Equation 11-22

Equation 11-23

R(s) + A/D Digital controller D(z) D/A Sensor Hk M(s) Amplifier and thrustors K T(S) Torque Satellite 1 Js (s) 8(1)