Given the second-order digital-filter transfer function

\[ D(z)=\frac{2 z^{2}-2.4 z+0.72}{z^{2}-1.4 z+0.98} \]

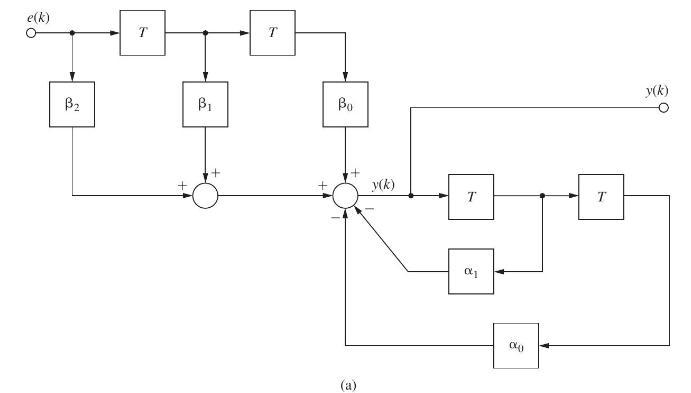
(a) Find the coefficients of the 3D structure of Fig. P2.8-1 such that \(D(z)\) is realized.

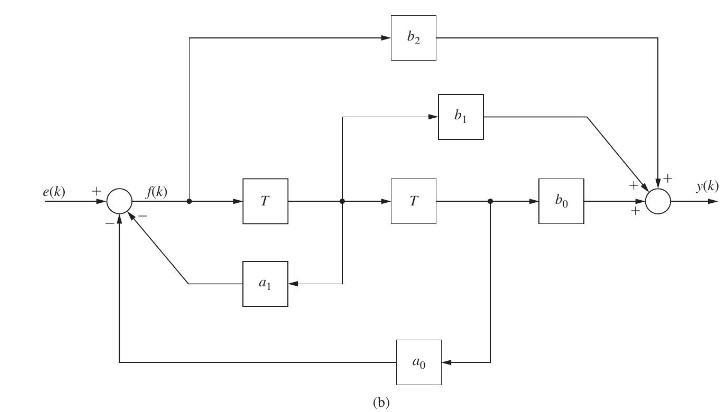
(b) Find the coefficients of the ID structure of Fig. P2.8-1 such that \(D(z)\) is realized.

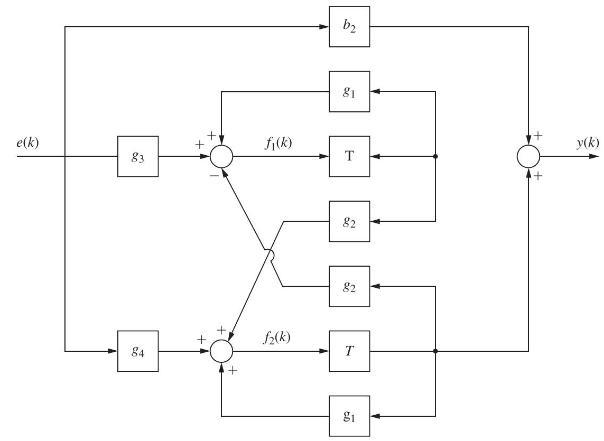
(c) Find the coefficients of the IX structure of Fig. P2.8-2 such that \(D(z)\) is realized. The coefficients are identified in Problem 2.8-2.

(d) Use MATLAB to verify the partial-fraction expansions in part (c).

(e) Verify the results in part (c) using Mason's gain formula.

Fig. P2.8-1

Problem 2.8-2

Shown in Fig. P2.8-2 is the second-order digital-filter structure 1X. This structure realizes the filter transfer function

\[
D(z)=b_{2}+\frac{A}{z-p}+\frac{A^{*}}{z-p^{*}}
\]

where \(p\) and \(p^{*}\) (conjugate of \(p\) ) are complex. The relationships between the filter coefficients and the coefficients in Fig. P2.8-2 are given by

\[
\begin{array}{ll}
g_{1}=\operatorname{Re}(p) & g_{3}=-2 \operatorname{Im}(A) \\
g_{2}=\operatorname{Im}(p) & g_{4}=2 \operatorname{Re}(A)
\end{array}
\]

Fig. P2.8-2

Transcribed Image Text:

e(k) T T B2 Bo (a) y(k) T T y(k)