Equivalence of several EC2SLS estimators. (a) Show that (A=[tilde{X}, bar{X}] ; B=) (left[X^{*}, tilde{X}ight]) and (C=left[X^{*}, bar{X}ight])
Question:
Equivalence of several EC2SLS estimators.
(a) Show that \(A=[\tilde{X}, \bar{X}] ; B=\) \(\left[X^{*}, \tilde{X}ight]\) and \(C=\left[X^{*}, \bar{X}ight]\) yield the same projection, i.e., \(P_{A}=P_{B}=P_{C}\) and hence the same EC2SLS estimator given by (7.11) (see Baltagi and Li (1992)).
(b) Show that \(P_{A} P_{X^{*}}=P_{X^{*}}\), and that \(P_{A}-P_{X^{*}}\) is idempotent. Use this result to prove that the \(\operatorname{avar}\left(\sqrt{n} \widehat{\beta}_{G 2 S L S}ight)-\operatorname{avar}\left(\sqrt{n} \widehat{\beta}_{E C 2 S L S}ight)\) is positive semidefinite, where avar denotes asymptotic variance and \(n=N T\). While this result may not be of consequence asymptotically since both estimators are asymptotically efficient. It may lead to smaller standard errors in finite samples. The intuition comes from the fact that extra instruments will in general lead to more efficient estimators, and in small samples, to lower standard errors. See problem 7.11 for an empirical illustration.
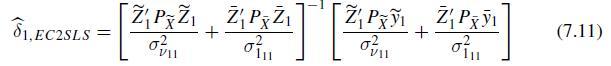
Step by Step Answer:






