Fuller and Battese (1973) transformation for the one-way random effects model. (a) Verify (2.17) and check that
Question:
Fuller and Battese (1973) transformation for the one-way random effects model.
(a) Verify (2.17) and check that \(\Omega^{-1} \Omega=I\) using (2.18).
(b) Verify that \(\Omega^{-1 / 2} \Omega^{-1 / 2}=\Omega^{-1}\) using (2.20) and (2.19).
(c) Pre multiply \(y\) by \(\sigma_{u} \Omega^{-1 / 2}\) from (2.20), and show that the typical element is \(y_{i t}-\theta \bar{y}_{i}\).
where
\(\theta=1-\left(\sigma_{v} / \sigma_{1}ight)\) .
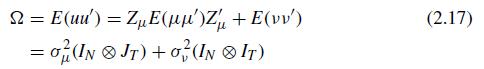
![]()


Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Question Posted:





