Unbiased estimates of the variance components: The one-way model. Using (2.21) and (2.22), show that (Eleft(widehat{sigma}_{1}^{2}ight)=sigma_{1}^{2}) and
Question:
Unbiased estimates of the variance components: The one-way model. Using (2.21) and (2.22), show that \(E\left(\widehat{\sigma}_{1}^{2}ight)=\sigma_{1}^{2}\) and \(E\left(\widehat{\sigma}_{v}^{2}ight)=\sigma_{v}^{2}\), Hint: \(E\left(u^{\prime} Q uight)=\) \(E\left\{\operatorname{tr}\left(u^{\prime} Q uight)ight\}=E\left\{\operatorname{tr}\left(u u^{\prime} Qight)ight\}=\operatorname{tr}\left\{E\left(u u^{\prime}ight) Qight\}=\operatorname{tr}(\Omega Q)\).
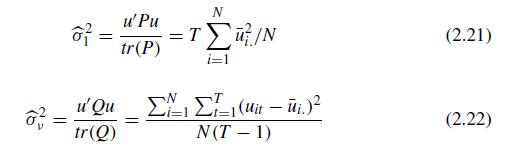
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Question Posted:





