Question: (Testing on the Boundary) The Student distribution contains the normal as a special case, suggesting that one can construct hypothesis test statistics for normality with

(Testing on the Boundary) The Student distribution contains the normal as a special case, suggesting that one can construct hypothesis test statistics for normality with this generalization. Suppose that {(%): 1., N) are i.i.d. Using the information in Exercise 15.18,

(a) create a score test for

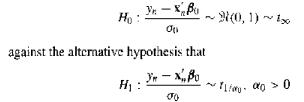
Y-XBo Ho N(0, 1)~1x against the alternative hypothesis that H:

(b) argue that the Wald and LR tests do not possess approximately chi-square distributions under Ho, and

(c) explain why the score test does not suffer from this difficulty.

Y-XBo Ho N(0, 1)~1x against the alternative hypothesis that H:

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Econometric Analysis Questions!

Location Income ($1,000) Urban 27 Rural 25 Suburban 25 Suburban 26 Rural 30 Urban 29 Rural 33 Urban 30 Suburban 32 Urban 34 Urban 35 Urban 40 Rural 30 Rural 33 Urban 42 Suburban 32 Urban 43 Urban 43...

A large national survey conducted in 1995 indicated that 18% of American adults had ever been tested for HIV at some point in their life. Suppose that in 2016 we take a simple random sample of 100...

Unit II Continuous Probability Distributions: The Normal Distribution Normal Dist1 Towards the Meaning of Continuous Probability Distribution Functions: When we introduced probabilities, we spoke of...

CHAPTER 9 Hypothesis Tests CONTENTS 9.4 POPULATION MEAN: UNKNOWN One-Tailed Test Two-Tailed Test Summary and Practical Advice 9.5 POPULATION PROPORTION Summary 9.6 HYPOTHESIS TESTING AND DECISION...

Asia Pacific Educ. Rev. (2012) 13:219-226 DOI 10.1007/s12564-011-9190-9 Performance and duration differences between online and paper-pencil tests Alper Bayazit Petek As kar Received: 10 September...

Assignment USE THE HARVARD REFERENCING SYSTEM THROUGHOUT THE REPORT Problem 1 (25 pts) The cost of 14 models of digitals cameras at a camera specialty store during 2014 was as follows: 340 450 450...

uantitative Methods for MBAs Homework 6 Angelo Mele This homework tests your understanding of inference. Each question is worth 20 points. Please print this paper and answer the question in the...

Center for Learning and Technology COURSE SYLLABUS PRINCIPLES OF STATISTICS STA-201-GS Course Syllabus PRINCIPLES OF STATISTICS STA-201-GS Thomas Edison State College May 2015 Course Essentials...

Project Part II: Data and Descriptive Statistics In this section you will expand your project to include your actual data set, descriptive statistics for your quantitative variables, linear...

Welcome! Please read this page (in particular) very carefully. Instructions You need to understand how to send your assignments (deliverables) to your instructor. The tabs (bottom of each sheet) in...

An unstable elementary particle called the eta meson has a rest mass of 549 MeV/c 2 and a mean lifetime of 7.00 1019 s. What is the uncertainty in its rest mass?

On June 1, Sidney Faultless of A. J. Faultless & Co., CPAs, noticed some disturbing information about the firms client, Hopkirk Company. A story in the local paper mentioned the indictment of Tony...

how to find the total debit and credit balances on the unadjusted trial balance?

A continuous function that is -1 for x -0.1, 1 for x 0.1, and is linear for -0.1