18.16 This exercise takes up the problem of missing data discussed in Section 9.2. Consider the regression model Yi = Xib + ui, i = 1,

c, n, where all variables are scalars and the constant term/intercept is omitted for convenience.

a. Suppose that the least squares assumptions in Key Concept 4.3 are satisfied. Show that the least squares estimator of b is unbiased and consistent.

b. Now suppose that some of the observations are missing. Let Ii denote a binary random variable that indicates the nonmissing observations;

that is, Ii = 1 if observation i is not missing and Ii = 0 if observation i is missing. Assume that {Ii, Xi, ui} are i.i.d.

i. Show that the OLS estimator can be written as

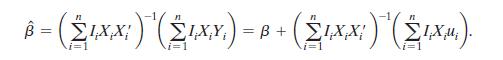
ii. Suppose that data are missing, “completely at random,” in the sense that Pr(Ii = 1 0Xi,ui) = p, where p is a constant. Show that b n is unbiased and consistent.
iii. Suppose that the probability that the ith observation is missing depends of Xi, but not on ui; that is, Pr(Ii = 1 0Xi, ui) = p(Xi).
Show that b n is unbiased and consistent.
iv. Suppose that the probability that the ith observation is missing depends on both Xi and ui; that is, Pr(Ii = 1 0Xi, ui) = p(Xi, ui). Is b n unbiased? Is b n consistent? Explain.

c. Suppose that b = 1 and that Xi and ui are mutually independent standard normal random variables [so that both Xi and ui are distributed N(0, 1)]. Suppose that Ii = 1 when Yi Ú 0, but Ii = 0 when Yi 6 0. Is b n unbiased? Is b n consistent? Explain.

== n B = (xx) (xx)=8+ (21xx)*(1x)- IXY B IXu