A regression of (Y_{t}) onto current, past, and future values of (X_{t}) yields [ Y_{t}=3.0+1.7 X_{t+1}+0.8 X_{t}-0.2
Question:
A regression of \(Y_{t}\) onto current, past, and future values of \(X_{t}\) yields
\[ Y_{t}=3.0+1.7 X_{t+1}+0.8 X_{t}-0.2 X_{t-1}+u_{t} \]
a. Rearrange the regression so that it has the form shown in Equation (17.25). What are the values of \(\theta, \delta_{-1}, \delta_{0}\), and \(\delta_{1}\) ?
b. i. Suppose that \(X_{t}\) is \(I(1)\) and \(u_{t}\) is \(I(1)\). Are \(Y\) and \(X\) cointegrated?
ii. Suppose that \(X_{t}\) is \(I(0)\) and \(u_{t}\) is \(I(1)\). Are \(Y\) and \(X\) cointegrated?
iii. Suppose that \(X_{t}\) is \(I(1)\) and \(u_{t}\) is \(I(0)\). Are \(Y\) and \(X\) cointegrated?
Equation (17.25)
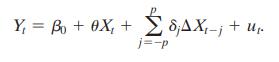
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Question Posted:





