Monte Carlo study. As an aid to understanding the probit model, William Becker and Donald Waldman assumed the following:

E(Y | X) = ˆ’1 + 3X

Then, letting Y_i = ˆ’1 + 3X + ε_i , where ε_i is assumed standard normal (i.e., zero mean and unit variance), they generated a sample of 35 observations as shown in the following table.

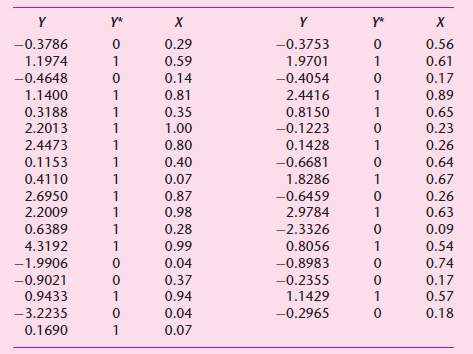
a. From the data on Y and X given in this table, can you estimate an LPM?

Remember that the true E(Y | X) = ˆ’1 + 3X.

b. Given X = 0.48, estimate E(Y | X = 0.48) and compare it with the true E(Y | X = 0.48). Note XÌ… = 0.48.

c. Using the data on Y* and X given in above table, estimate a probit model. You may use any statistical package you want. The authors€™ estimated probit model is the following:

YÌ‚^ˆ—_i = ˆ’0.969 + 2.764X_i

Find out the P(Yˆ— = 1 | X = 0.48), that is, P(Y₁ > 0 | X = 0.48). See if your answer agrees with the authors€™ answer of 0.64.

d. The sample standard deviation of the X values given in above table is 0.31. What is the predicted change in probability if X is one standard deviation above the mean value, that is, what is P(Yˆ— = 1 | X = 0.79)? The authors€™ answer is 0.25.

Transcribed Image Text:

х y* -0.3786 -0.3753 0.29 0.56 1.1974 1 0.59 1.9701 1 0.61 -0.4648 0.14 -0.4054 0.17 1.1400 0.81 2.4416 1 0.89 0.3188 1 0.35 0.8150 -0.1223 0.1428 0.65 2.2013 1.00 0.23 2.4473 1 0.80 1 0.26 0.40 0.1153 1 -0.6681 0.64 0.4110 1 0.07 1.8286 0.67 2.6950 1 0.87 -0.6459 0.26 2.2009 1 0.98 2.9784 0.63 0.6389 1 0.28 -2.3326 0.09 0.54 4.3192 1 0.99 0.8056 0.04 -1.9906 -0.8983 0.74 -0.9021 0.37 -0.2355 0.17 0.9433 0.94 1.1429 0.57 0.04 -3.2235 -0.2965 0.18 0.1690 0.07