Suppose that you work in the admissions office of a college that doesn€™t allow prospective students to apply by using the Common Application.9 How might you go about estimating the number of extra applications that your college would receive if it allowed the use of the Common Application? An econometric approach to this question would be to build the best possible model of the number of college applications and then to examine the estimated coefficient of a dummy variable that equaled one if the college in question allowed the use of the €œcommon app€ (and zero otherwise).

For example, if we estimate an equation using the data in Table 2.3 for high-quality coed national liberal arts colleges, we get:

N = 49 R² = .724 RÌ…² = .705

Where:

APPLICATION_i = the number of applications received by the ith college in 2007

SIZE_i = the total number of undergraduate students at the ith college in 2006

RANK_i = the U.S. News¹⁰ rank of the ith college (1 = best) in 2006

COMMONAPP_i = a dummy variable equal to 1 if the ith college allowed the use of the Common Application in 2007 and 0 otherwise.

Table 2.3 Data for the College Application Example

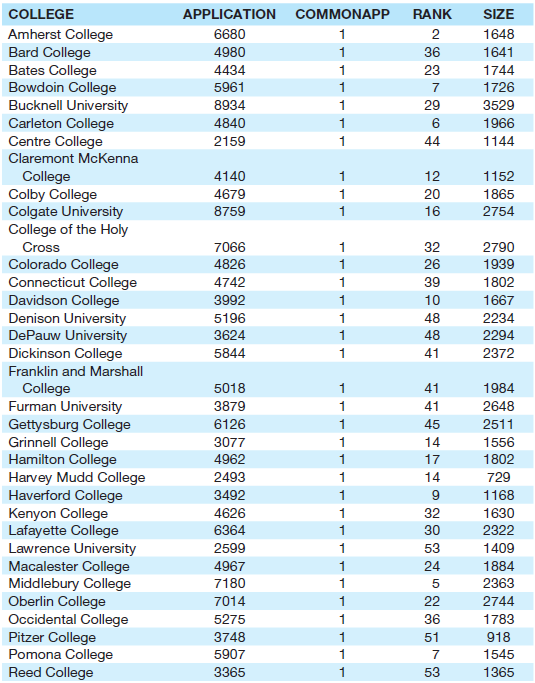
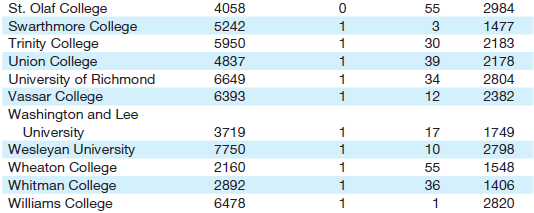
a. Take a look at the signs of each of the three estimated regression coefficients. Are they what you would have expected? Explain.

b. Carefully state the real-world meaning of the coefficients of SIZE and RANK. Does the fact that the coefficient of RANK is 15 times bigger (in absolute value) than the coefficient of SIZE mean that the ranking of a college is 15 times more important than the size of that college in terms of explaining the number of applications to that college? Why or why not?

c. Now carefully state the real-world meaning of the coefficient of COMMONAPP. Does this prove that 1,222 more students would apply if your college decided to allow the Common Application? Explain.

d. Now use the same data and estimate Equation 2.18 again without the COMMONAPP variable. What is the new RÌ…²? Does RÌ…² go up or down when you drop the variable? What, if anything, does this change tell you about whether COMMONAPP belongs in the equation?

Transcribed Image Text:

COLLEGE APPLICATION COMMONAPP RANK SIZE Amherst College Bard College Bates College Bowdoin College Bucknell University Carleton College Centre College 6680 2 1648 4980 36 1641 4434 23 1744 5961 1726 7 8934 29 3529 4840 1966 2159 44 1144 Claremont McKenna College Colby College Colgate University College of the Holy 4140 12 1152 4679 20 1865 8759 16 2754 Cross 7066 32 2790 Colorado College Connecticut College Davidson College Denison University DePauw University Dickinson College 4826 26 1939 4742 39 1802 3992 10 1667 5196 48 2234 3624 1 48 2294 2372 5844 Franklin and Marshall 5018 1984 College Furman University Gettysburg College Grinnell College Hamilton College Harvey Mudd College Haverford College Kenyon College Lafayette College Lawrence University Macalester College Middlebury College Oberlin College Occidental College Pitzer College Pomona College Reed College 41 3879 41 2648 6126 45 2511 3077 14 1556 4962 17 1802 2493 14 729 3492 1168 4626 6364 1630 32 30 2322 2599 53 1409 4967 1 24 1884 2363 7180 7014 22 2744 5275 36 1783 3748 51 918 5907 1545 3365 53 1365 Rhodes College 3709 1 45 1662 Sewanee-University of the South Skidmore College St. Lawrence University 2424 6768 4645 34 48 1498 2537 2148 57