The book's website provides code that will simulate a data set we can use to explore the effects of including post-treatment variables. (Stata code is in Ch7_PostTreatmentSimulation.do; \(\mathrm{R}\) code is in Ch7_PostTreatmentSimulation.R).

The first section of code simulates what happens when \(X_{1}\) (the independent variable of interest) affects \(X_{2}\), a post-treatment variable as in Figure 7.8. Initially, we set \(\gamma_{1}\) (the direct effect of \(X_{1}\) on \(Y\) ), \(\alpha\) (the effect of \(X_{1}\) on \(X_{2}\) ), and \(\gamma_{2}\) (the effect of \(X_{2}\) on \(Y\) ) all equal to 1 .

FIGURE 7.8: 

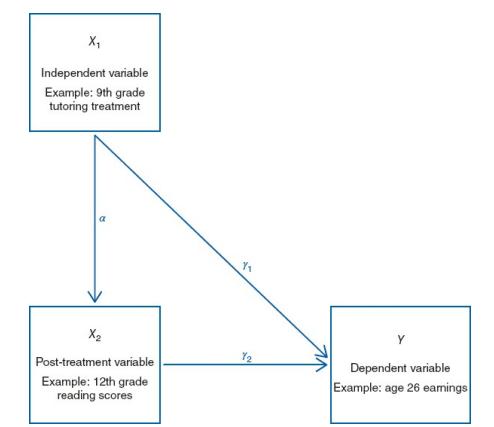
(a) Estimate a bivariate model in which \(Y=\beta_{0}+\beta_{1} X_{1}\). What is your estimate of \(\beta_{1}\) ? How does this estimate change for (i) \(\gamma_{1}=0\), (ii) \(\gamma_{2}=0\) (setting \(\gamma_{1}\) back to 1 ), and (iii) \(\alpha=1\) (setting \(\gamma_{1}\) and \(\gamma_{2}\) equal to 1 ).

(b) Estimate a multivariate model in which \(Y=\beta_{0}+\beta_{1} X_{1}+\beta_{2} X_{2}\). What is your estimate of \(\beta_{1}\) ? How does this estimate change for (i) \(\gamma_{1}=0\), (ii) \(\gamma_{2}=0\) (setting \(\gamma_{1}\) back to 1), and (iii) \(\alpha=1\) (setting \(\gamma_{1}\) and \(\gamma_{2}\) equal to 1 ).

(c) Come up with a real-world example with \(\mathrm{X}_{1}, \mathrm{X}_{2}\), and \(\mathrm{Y}\) for an analysis of interest to you.
The second section code adds an unmeasured confounder, \(\mathrm{U}\), to the simulation. Refer to Figure 7.9. Initially, we set \(\alpha\) (the effect of \(X_{1}\) on \(X_{2}\) ), \(ho_{1}\) (the effect of \(U\) on \(X_{2}\) ), and \(ho_{2}\) (the effect of \(U\) on \(Y\) ) all equal to 1 .

FIGURE 7.9: 

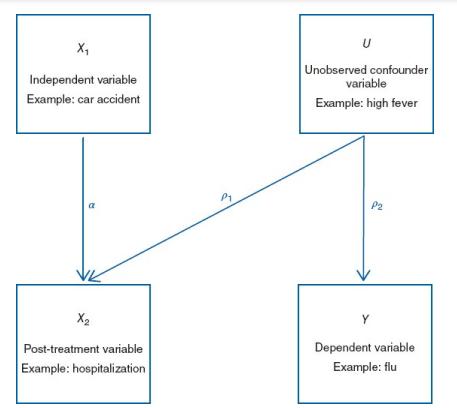
(d) Estimate a bivariate model in which \(Y=\beta_{0}+\beta_{1} X_{1}\). What is your estimate of \(\beta_{1}\) ? How does this estimate change for (i) \(\alpha_{1}=0\) (ii) \(ho_{1}\) \(=0\) (setting \(\alpha_{1}\) back to 1 ), and (iii) \(ho_{2}=1\) (setting \(\alpha_{1}\) and \(ho_{1}\) equal to 1 )?

(e) Estimate a multivariate model in which \(Y=\beta_{0}+\beta_{1} X_{1}+\beta_{2} X_{2}\). What is your estimate of \(\beta_{1}\) ? How does this estimate change for (i) \(\alpha_{1}=0\) (ii) \(ho_{1}=0\) (setting \(\alpha_{1}\) back to 1 ), and (iii) \(ho_{2}=1\) (setting \(\alpha_{1}\) and \(ho_{1}\) equal to 1 ).

(f) Come up with a real-world example with \(\mathrm{X}_{1}, \mathrm{X}_{2}\), U, and \(\mathrm{Y}\) for an analysis of interest to you.
(g) [Advanced] Create a loop in which you run these simulations 100 times for each exercise, and record the average value of the parameter estimates.

Transcribed Image Text:

X Independent variable Example: 9th grade tutoring treatment 11 X2 Post-treatment variable Example: 12th grade reading scores Dependent variable Example: age 26 eamings