Consider three villagers that live for ten periods and have linear, additive utility functions as follows:

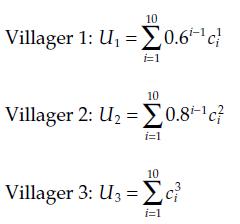
where c_iⁿ is the consumption (both of durable and nondurable) at time i of villager n, and 0.6, 0.8, and 1 are respectively the discount factors of villager 1, 2, 3. Note that villager 1 is the most impatient, and villager 3 the least impatient. Assume that at each period, each villager earns y = \($140,\) and the subsistence level of consumption for all of them is c = \($80,\) so the maximum amount that each villager can save at each period is (y - c). A durable good costs B = \($360,\) and if villagers can buy it, they can use it over the next two periods for an extra amount θ = \($2,000\) each period. Assume a ROSCA that is organized as follows. For the first meeting, the pot will go to the villager that pays an amount A1 = \($1,000.\) If there are at least two villagers that are willing to pay for the pot, then the pot will go to the villager that can give the highest bid the next period. Those participant villagers that do not take the pot can have one-half of the bid. At the second meeting, the one that got the pot in first meeting is excluded from playing. Again, the pot will go to the participant villager that pays the highest bid, which is greater than A2 = \($400,\) and the bid will be shared equally between the other two participant villagers. At the third meeting, the remaining villager will get the pot. Which villager will get the pot at the first meeting, at the second meeting, and the third meeting? (Assume that if the villager does not turn up to make her contributions after having obtained the pot, she will be severely punished, and her utility will be -∞.)

Transcribed Image Text:

10 Villager 1: U =0.6c E=1 10 i-1 2 Villager 2: U2 = 0.81c i=1 10 Villager 3: U3c = i=1